29.Размещения. Перестановки. Сочетания (без повторений).

Перестановки без повторений

Перестановки в ряд

Перестановкой из 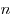элементов (или 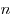-перестановкой) называется 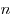-элементное упорядоченное множество, составленное из элементов 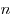-элементного множества.

Иначе: Перестановкой из 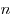элементов (или 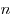-перестановкой) называется размещение из 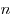элементов по 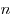без повторений.

Число перестановок из 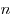элементов без повторений обозначается P_n от французского словаperturbation.

Теорема: число способов расположить в ряд 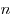различных объектов есть

$P_n = n(n - 1)(n - 2) \cdot \ldots \cdot 2 \cdot 1 = n!$

Замечание: Рекуррентная формула: $P_n = nP_{n - 1}$ .

Перестановки симметричных объектов

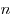различных предметов можно расположить по кругу (n - 1)! способами, а если их можно еще и переворачивать, то $\frac{{(n - 1)!}}{2}$ различными способами.

Размещения без повторений

Подсчитаем количество способов расположить 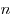различных элементов по различным позициям ( k < n ). Такие расположения называются размещениями, а их количество, от французского слова arrangement обозначается A_n^k . В случае, если k = n количество предметов совпадает с количеством имеющихся мест, и это уже изученная задача о числе перестановок.

Если из 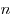объектов выбирают штук, то число выборов последнего объекта есть n - k невыбранных объектов, что означает наличие n - k + 1 возможности выбора последнего выбранного объекта. То же, другими словами: после выбора первых k - 1 элемента остается выбрать n - (k - 1) = n - k + 1 элемент.

Теорема: число размещений 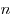различных элементов по различным позициям есть

$A_{\,n}^{\,k} = n(n - 1)(n - 2) \ldots (n - k + 1)$ ,

или, в терминах факториалов,

$A_n^k = \frac{{n!}}{{(n - k)!}}$ .

Примечание: заметим, что в случае, когда число мест, по которым размещают предметы, совпадает с количеством самих предметов, т. е. когда k = n , рассматриваемая задача становится задачей о числе перестановок. В нашем случае при этом мы получаем в знаменателе дроби ноль факториал, и для того, что бы разные формулы, соответствующие одной и той же задаче, приводили к одинаковым результатам, полагают, что 0! = 1 .

Сочетания

Подсчитаем количество способов, которыми можно выбрать из 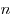различных предметов. Такие выборки называются сочетаниями, а их количество обозначается $C_n^{\,k}$ .

При k < n , выбрать k предметов из n можно $A_{\,n}^{\,k}$ способами, переставляя их P_k способами:

$C_n^{\,k} = \frac{{A_{\,n}^{\,k} }}{{P_k }} = \frac{{n!}}{{(n - k)!\,\, \cdot k!}}$ .

Рекуррентная формула: $C_m^n = C_m^{n - 1} \frac{{m - n + 1}}{n}$ .

Свойства сочетаний: $C_m^n = C_m^{m - n}$ ; $\;C_m^n + C_m^{n + 1} = C_{m + 1}^{n + 1}$ .