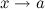(Правило Лопиталя).
Пусть функции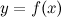 
и 
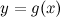удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки 
, кроме, может быть, самой точки ;
2) 
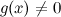и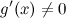 
в этой окрестности;
3) 
;
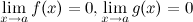4) 
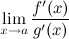существует конечный или бесконечный.
Тогда существует и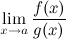 
, причем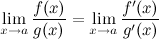 
Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.
Правило Лопиталя распространяется на случай неопределенности типа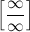 
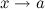
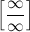при 
при 
