Действия с комплексными числами. Теорема о корнях многочлена

. Арифметические операции.Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры.

Пусть 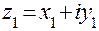, 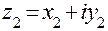. Тогда

сумма ,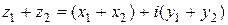

разность ,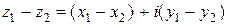

произведение ,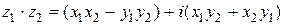

частное (при )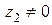

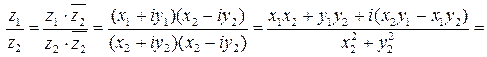
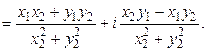
Умножение и деление комплексных чисел в тригонометрической форме.Пусть числа 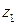и 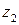заданы в тригонометрической форме: 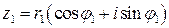, 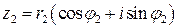. Перемножим их:

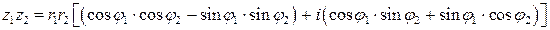Вспоминая формулы для косинуса и синуса суммы двух углов, получаем

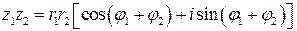. (1)

Мы видим, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Геометрический смысл этой операции: представляя числа 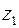и 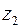векторами на комплексной плоскости, исходящими из нуль-точки, видим, что вектор 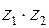получается из вектора 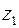«растяжением» в 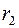раз и поворотом на угол .

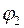Для частного получаем формулу:

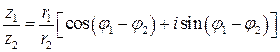. (2)

Возведение комплексного числа в степень.Из формулы (1) следует, что возведение в степень 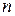комплексного числа 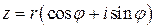производится по правилу

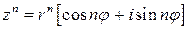. (3)

Формула Муавра:

$z^n=$ $r^n(\cos(n\varphi)+i\sin(n\varphi)).$

Доказательство. Разобьем доказательство на 3 этапа.

1) Пусть – натуральное число. Так как комплексное числоимеет модуль, то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.

2) Пусть теперь . Тогда

, ч.т.д.

3) Пусть , где– натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в поле комплексных чисел, имеем:

Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).

Теорема доказана.