Комплексным числом называется выражение вида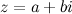

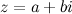Действительное число называется действительной частью комплексного числа и обозначается .

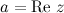Действительное число 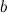называется мнимой частью числа 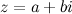и обозначается .

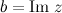Формы записи комплексного числа

Алгебраическая форма комплексного числа

Запись комплексного числа в виде 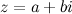, где и 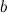- действительные числа, называется алгебраической формой комплексного числа.

Например.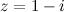

Подробнее о данной форме записи комплексных чисел по ссылке →

Тригонометрическая форма комплексного числа

Если 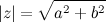- модуль комплексного числ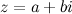а , а 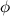- его аргумент, то тригонометрической формой комплексного числа называется выражение

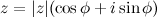
Показательная форма комплексного числа

Показательной формой комплексного числа 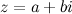называется выражение

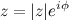
Заметим, что показательную и тригонометрическую формы комплексного числа связывает формула Эйлера:

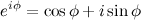
Равенство и сравнение комплексных чисел.

         Два комплексных числа считаются равными, если у них равны вещественные и мнимые части:

.

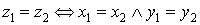         Но вот операции типа «больше» и «меньше» для комплексных чисел не имеют смысла, то есть бессмысленно писать 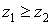 или 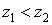. Совершенно непонятно, что больше  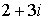или 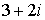. Комплексные числа не упорядочены.