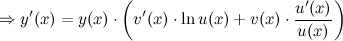Логарифмическое дифференцирование
Для функций вида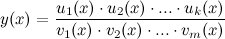 
для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.
Суть метода логарифмического дифференцирования
Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция 
. Прологарифмируем левую и правую части данного выражения:
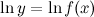
Далее продифференцируем полученное равенство при условии, что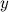 
является функцией от 
, то есть найдем производную сложной функции:
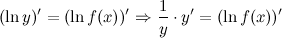
А тогда, выражая искомую производную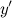 
, в результате имеем:
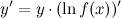
Производная показательно-степенной функции
Рационально использовать логарифмическое дифференцирование и при нахождении производной показательно-степенной (или степенно-показательной) функции или "функции в степени функция", то есть в случае, когда заданная функция имеет вид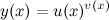 
. Логарифмируем левую и правую часть:
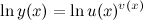
далее по свойствам логарифма
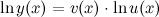
Тогда
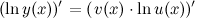
Производную в левой части равенства находим как производную сложной функции, а в правой - как производную произведения:
