Дифференцирование параметрически заданной функции. Дифференцирование неявно заданных функции.

Пусть функция 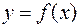задана параметрически:

.

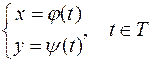Найдем первую производную функции 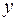по переменной 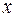, то есть

.

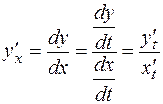Т.е. .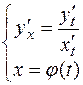

Найдем вторую производную от функции 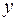по переменной 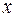. Прямое дифференцирование функции 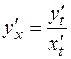возможно только по параметру 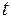и даст в результате смешанную производную 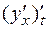. Поэтому для нахождения второй производной от функции 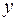по переменной 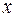предварительно представим ее в виде:

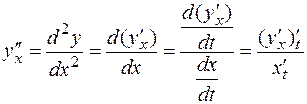
Тогда .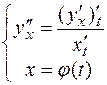

Аналогично находится третья производная:

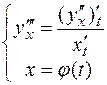
и производные высших порядков.

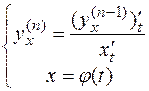
Дифференцирование неявно заданных функции

Пусть уравнение 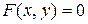определяет 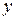как некоторую функцию от 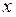. Если в это уравнение подставить вместо у функцию 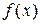, то получим тождество

.

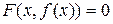Придадим 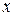приращение 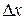, тогда значению аргумента будет соответствовать значение функции 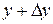, но с другой стороны

.

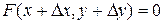Разность 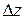также равна нулю:

.

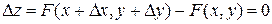Как было показано выше, ее полное приращение в этой точке можно представить в виде

.

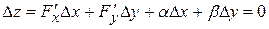Разделим последнее равенство на :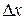

.

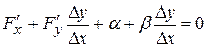Откуда

.

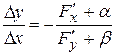Перейдя к пределу, получим формулу вычисления производной функции, заданной неявно:

.

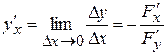Аналогично можно вычислить частные производные неявной функции 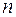переменных по всем ее аргументам.

Например, для функции 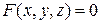справедливо:

, .
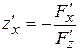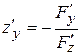