Функция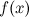 
называется непрерывной в точке 
, если:
- функция 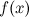определена в точке и ее окрестности;
- существует конечный предел функции 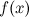в точке ;
- это предел равен значению функции в точке , т.е.
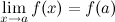
Понятие непрерывности функции в точке
Основные понятия и определения
Определение
Замечание
При нахождении предела функции 
, которая является непрерывной, можно переходить к пределу под знаком функции, то есть
Приращение аргумента и функции
Рассмотрим функцию , которая определена в некотором интервале 
и рассмотрим произвольную точку 
из этого интервала: 
.
Определение
Приращением аргумента 
в точке называется разность 
Замечание. Из последнего равенства легко увидеть, что 
.
Приращением функции 
в точке называется разность соответствующих значений функции 
или, используя равенство из выше приведенного замечания, будем иметь:
Теорема
Функция непрерывна в точке тогда и только тогда, когда бесконечно малому приращению аргумента 
соответствует бесконечно малое приращение функции 
:
Полезные теоремы о непрерывности функции
Теорема
Если функции и 
непрерывны в точке , то функции 
, 
, 
также непрерывны в точке .
Пусть функция 
задана на множестве 
, а 
- множество значений этой функции. Пусть на множестве задана функция 
. Тогда говорят, что на множестве задана композиция функций (или сложная функция) 
.
Теорема
Пусть функция непрерывна в точке , а функция непрерывна в точке 
. Тогда композиция функций непрерывна в точке .
Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
Критерий непрерывности функции
Функция y = f(x) непрерывна в точке x0 тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
= 
