Свойство 1. Сумма конечного числа бесконечно малых функций является бесконечно малой функцией.
Д о к а з а т е л ь с т в о.
Пусть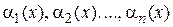 
бесконечно малые функции при 
.
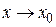По определению для этих бесконечно малых функций запишем:
;
;
………………………………………………………………………………………..
.
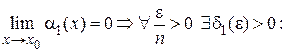
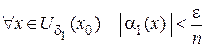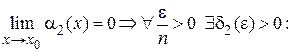
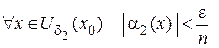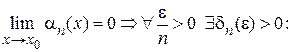
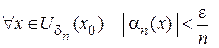Если принять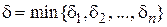 
, то 
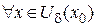имеет место неравенство:
,
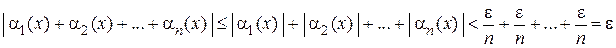т. е. сумма бесконечно малых функций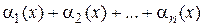 
является бесконечно малой функцией.
Свойство 2. Произведение бесконечно малой функции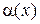 
на ограниченную функцию 
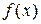является бесконечно малой функцией.
Д о к а з а т е л ь с т в о. Пусть a(х) бесконечно малая функция, т. е.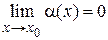 
, а функция f(x) в окрестности точки 
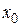ограничена, т. е. 
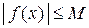, где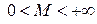 
. Так как 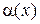- бесконечно малая функция, то как бы мало ни было число e, в том числе и равное 
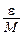, существует такая d-окрестность 
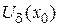, что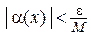 
.
Поэтому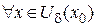 
.
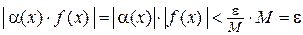Следствие 1. Произведение бесконечно малой функции 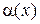на постоянную величину С является бесконечно малой функцией, т. е. 
.
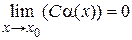Следствие 2. Произведение бесконечно малых функци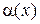й и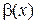 
является бесконечно малой функцией.
Свойство 3. Частное от деления бесконечно малой функции 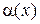на функцию 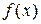, предел которой отличен от нуля ( 
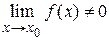) является бесконечно малой функцией.
Д о к а з а т е л ь с т в о. Пусть a(x) бесконечно малая функция, т. е.
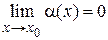и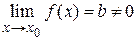 
. Докажем, что 
.
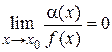Так как 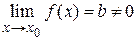, то существует такая d-окрестность , что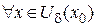 
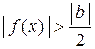, а следовательно 
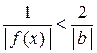. Это значит, что в d-окрестности точки 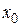функция 
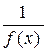ограничена. По свойству 2 произведение бесконечно малой a(x) на ограниченную функцию 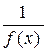является бесконечно малой, т. е. .
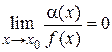Основные свойства бесконечно малых функций
1° Сумма конечного числа б.м функций является функцией б.м.
2° Произведение б.м функции на ограниченную есть функция б.м.
3° Произведение двух б.м функций есть функция б.м.
4° Произведение б.м функции на константу является б.м функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6° Функция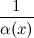 
, обратная к б.м функции 
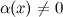, есть функция бесконечно большая. Верно и обратное.
