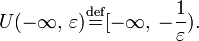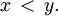Несобственные точки числовой прямой. Дополним множество вещественных чисел тремя новыми объектами (-∞, +∞, ∞), которые определим через систему их окрестностей. 
Определения.
3.3.1. Несобственной точкой -∞ будем называть объект, К-окрестность которого - множество UK(-∞) ={x| x < K}.
Для ∀у ∈ R выполняется -∞ < у.
3.3.2. Несобственной точкой +∞ будем называть объект, К-окрестность которого - множество UK(+∞) ={x| x > K}.
Для ∀у ∈ R выполняется у < +∞.
3.3.3. Несобственной точкой ∞ будем называть объект, К-окрестность которого - множество UK(∞) ={x| |x| > K} = UK(-∞)∪UK(+∞).
| Предельная точка |
|
1. Предельная точка множества. Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р. Оказывается, в любой окрестности предельной точки содержится бесконечное число точек множества М. Сама же предельная точка может как принадлежать, так и не принадлежать множеству М. 2. Предельная точка числовой последовательности. Так называют (если он существует) частичный предел последовательности {xn} т.е. такое число с, что существует подпоследовательность {xnk} данной последовательности, для которой |
Определение 1. Число a называется предельной точкой последовательности {xn}, если из последовательности {xn} можно выделить подпоследовательность, сходящуюся к a.
Определение 2. Число a называется предельной точкой последовательности {xn}, если в любой e-окрестности точки a содержится бесконечно много членов последовательности {xn}.
Утверждение. Определения 1 и 2 эквивалентны.
В самом деле, пусть a - предельная точка последовательности {xn} по первому определению, тогда существует подпоследовательность 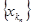 ® a, и в любой e-окрестности точки a содержится бесконечно много членов последовательности {xn}, а это и означает, что точка a является предельной точкой последовательности по определению 2.
® a, и в любой e-окрестности точки a содержится бесконечно много членов последовательности {xn}, а это и означает, что точка a является предельной точкой последовательности по определению 2.
Пусть {xn} - числовая последовательность, и пусть k1 , k2 , … , kn , … - возрастающая последовательность, элементами которой являются натуральные числа. Выберем из последовательности {xn} элементы с номерами k1 , k2 , … , kn , … , получим вот такую последовательность: 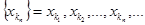 , она называется подпоследовательностью последовательности {xn}. Отметим, что kn ³ n. Примеры подпоследовательностей:
, она называется подпоследовательностью последовательности {xn}. Отметим, что kn ³ n. Примеры подпоследовательностей:
1) {x2n} = x2 , x4 , … , x2n , …
2) 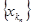 = x1 , x3 , x7 , x13 , …
= x1 , x3 , x7 , x13 , …
3) {xn} - сама последовательность.
Предельная точка множества. Предел функции в точке
Пусть . Число
называется предельной точкой множества X, если
Из определения следует, что любая окрестность точки x0 содержит точку из множества X, отличную от x0. Сама точка x0 может принадлежать, а может и не принадлежать множеству X.
Значение +∞ есть предельная точка множества X, если
Значение -∞ предельная точка множества X, если
Точка , не являющаяся предельной точкой множества X, называется изолированной точкой множества X, т. е.
Число называется предельной точкой множества
, если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x0. (Данное определение и определение, указанное в самом начале эквивалентны)
ПОНЯТИЕ ОКРЕСТНОСТИ
ОКРЕСТНОСТЬЮ ТОЧКИ Хо называется любой интервал, содержащий эту точку.
ПРОКОЛОТОЙ ОКРЕСТНОСТЬЮ т. Хо называется окрестность т. Хо, из которой выброшена сама точка.
ОКРЕСТНОСТЬЮ "+" БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (а;+) .
ОКРЕСТНОСТЬЮ "-" БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (- ;b) .
ОКРЕСТНОСТЬЮ БЕСКОНЕЧНОСТИ называется объединение двух любых окрестностей + и - .
Функция f(х) называется бесконечно малой в окрестности т. Хо, если для любого числа >0 существует проколотая окр. т. Хо такая, что для любого числа Х, принадлежащего прокол. окр. т. Хо выполняется неравенство іf(х) і<.
>0 U U => іf(x) і< Число А называется пределом ф-ции f(х) в т. Хо, если в некоторой прок. окр. этой точки ф-цию f(х) можно представить в виде f(х) =А+ (х) , где (х) -бесконечно малое в окрестности т. Хо.
limf(x) =А Ф-ция f(х) называется непрерывной в т. Хо, если в некоторой окр. т. Хо эту ф-цию можно представить в виде: f(х) =f(х) + (х) , где (х) -б. м. в окр. т. Хо.
Иными словами, f(х) -непрерывна в т. Хо, если она в этой точке имеет предел и он равен значению ф-ции.
Напомним определения некоторых основных подмножеств действительных чисел. Если 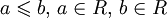 , то множество
, то множество 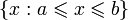 называется отрезком расширенной числовой прямой R и обозначается через
называется отрезком расширенной числовой прямой R и обозначается через ![[a,\;b]](http://dic.academic.ru/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , то есть
, то есть
![[a, b]\stackrel{\mathrm{def}}{=}\{x: a\leqslant x\leqslant b\}, a\in \overline{R}, b\in \overline{R} .](http://dic.academic.ru/pictures/wiki/files/49/1662dc0d24e95c9e84df5096ca46bc47.png)
В случае 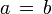 отрезок
отрезок ![[a\,,\, b]](http://dic.academic.ru/pictures/wiki/files/57/9e070be9629f1dc33d14853dc3686dc4.png) состоит из одной точки.
состоит из одной точки.
Если 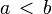 , то множество
, то множество 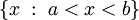 называется интервалом и обозначается через
называется интервалом и обозначается через 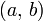 , т.е.
, т.е.
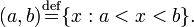
Интервал 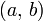 называется внутренностью отрезка
называется внутренностью отрезка ![[a,\, b].](http://dic.academic.ru/pictures/wiki/files/53/5ac2bbff3671a6b77208619abc7a33b4.png)
Множестваи
называются полуинтервалами.
Отрезки ![[a,\, b]](http://dic.academic.ru/pictures/wiki/files/100/d2524b9940ce1c636bfb26ae09a941d2.png) , интервалы
, интервалы 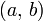 и полуинтервалы
и полуинтервалы ![[a,\, b), \,(a,\, b]](http://dic.academic.ru/pictures/wiki/files/102/f23906a47b274318ffe7e8ee9d01084a.png) называются промежутками, а точки a и b - их концами: a - левым концом, а b - правым, а точки x такие, что
называются промежутками, а точки a и b - их концами: a - левым концом, а b - правым, а точки x такие, что 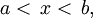 - их внутренними точками.
- их внутренними точками.
Если a и b конечны, т.е. 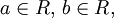 то промежуток с концами a и b называется также конечным промежутком, а число b ? a - его длиной. Если хотя бы одно из a и b является бесконечным, то промежуток с концами a и b называется бесконечным.
то промежуток с концами a и b называется также конечным промежутком, а число b ? a - его длиной. Если хотя бы одно из a и b является бесконечным, то промежуток с концами a и b называется бесконечным.
Замечание 1. Промежутки всех типов расширенной числовой прямой обладают следующим свойством: если точкипринадлежат некоторому промежутку с концами
и
то и весь отрезок
принадлежит этому промежутку.
Для промежутка каждого типа это непосредственно следует из его определения.
Важным понятием для дальнейшего является понятие  - окрестности точки расширенной числовой прямой. В случае
- окрестности точки расширенной числовой прямой. В случае 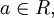 т.е. когда a является действительным числом,
т.е. когда a является действительным числом,  - окрестностью
- окрестностью 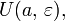 [1]
[1]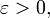 а числа a называется интервал
а числа a называется интервал 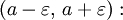
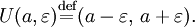
Если же 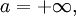 то
то
а если 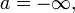 то
то
Таким образом, во всех случаях, т.е. когда a - действительно число и когда a - одна из бесконечностей 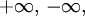 при уменьшении числа
при уменьшении числа  соответствующие
соответствующие  - окрестности
- окрестности 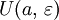 уменьшаются: если
уменьшаются: если 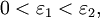 то
то 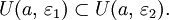
Иногда бывает удобно пополнить множество действительных чисел не двумя, а одной бесконечностью (без знака) 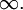 Ее
Ее  - окрестность
- окрестность 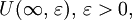 определяется равенством
определяется равенством
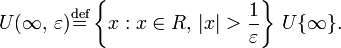
Иначе говоря,  - окрестность
- окрестность 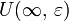 состоит из двух бесконечных интервалов
состоит из двух бесконечных интервалов 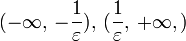 и самого элемента
и самого элемента 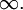 Этот элемент также называется иногда бесконечно удаленной точкой числовой прямой. В отличие от бесконечностей со знаком
Этот элемент также называется иногда бесконечно удаленной точкой числовой прямой. В отличие от бесконечностей со знаком 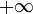 и
и 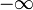 бесконечность
бесконечность 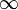 без знака не связана с действительными числами отношением порядка.
без знака не связана с действительными числами отношением порядка.
Всякая  - окрестность конечной или бесконечно удаленной точки числовой прямой называется ее окрестностью и часто обозначается просто через U(a). Иногда мы будем обозначать окрестность и другими буквами, например V, W.
- окрестность конечной или бесконечно удаленной точки числовой прямой называется ее окрестностью и часто обозначается просто через U(a). Иногда мы будем обозначать окрестность и другими буквами, например V, W.
Нередко с определенными выше окрестностями бесконечностей в пополнениях ими множества действительных чисел иногда рассматривают и окрестности бесконечностей 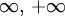 и
и 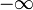 в самом множестве действительных чисел:
в самом множестве действительных чисел: 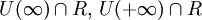 и
и 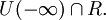 Сами бесконечности, конечно, уже не попадают в эти окрестности.
Сами бесконечности, конечно, уже не попадают в эти окрестности.
Лемма У любых двух различных точек расширенной числовой прямой (расширенной с помощью двух бесконечностей со знаком или при помощи только одной бесконечности без знака) существуют непересекающиеся окрестности.
Доказательство. Рассмотрим сначала случай расширенной числовой прямой R, полученной добавлением к множеству действительных чисел R двух бесконечностей со знаком. Покажем, что для любых 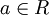 и
и 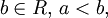 существуют такие
существуют такие 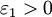 и
и 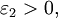 что
что 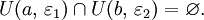 В самом деле, если a и b - действительные числа, то можно взять
В самом деле, если a и b - действительные числа, то можно взять 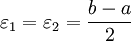 (рис. 1, а)[2] Если a - действительное число, а
(рис. 1, а)[2] Если a - действительное число, а 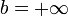 , то в качестве указанных
, то в качестве указанных 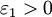 и
и 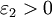 подходят, например,
подходят, например, 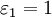 и
и 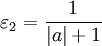 (рис. 1, б). Если
(рис. 1, б). Если 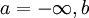 - действительное число, то можно взять
- действительное число, то можно взять 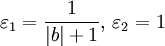 (рис. 1, в). Наконец, если
(рис. 1, в). Наконец, если 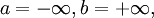 то при произвольном
то при произвольном 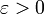 окрестности
окрестности 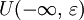 и
и 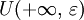 не пересекаются (рис. 1, г). Если же числовая прямая R дополнена лишь одной бесконечностью
не пересекаются (рис. 1, г). Если же числовая прямая R дополнена лишь одной бесконечностью 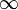 , то достаточно рассмотреть лишь случай
, то достаточно рассмотреть лишь случай 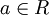 и
и 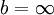 (так как случай
(так как случай 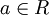 и
и 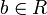 рассмотрен выше), в котором можно снова (как при
рассмотрен выше), в котором можно снова (как при 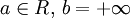 ) взять
) взять 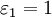 , а
, а 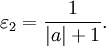
Замечание 2. В случаеи их непересекающихся окрестностей
для любых
и
очевидно, справедливо неравенство
Его справедливость устанавливается непосредственной проверкой во всех возможных здесь случаях, т.е. при 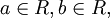 при
при 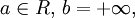 при
при 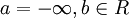 и при
и при 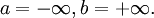 Легко убедиться, что пересечение двух окрестностей точки (конечной или бесконечно удаленной) является также окрестностью этой точки.
Легко убедиться, что пересечение двух окрестностей точки (конечной или бесконечно удаленной) является также окрестностью этой точки.



![U(+\infty,\, \varepsilon)\stackrel{\mathrm{def}}{=}({1\over \varepsilon} ,\, +\infty],](http://dic.academic.ru/pictures/wiki/files/99/c074324d06f100920bcc0382655bbe8b.png)