Карты Карно – это графическое изображение таблиц истинности.
Пусть задана функция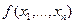 
. Подмножество элементов 
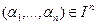, в которых 
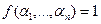, называется носителем функции f и обозначается через supp(f). Конечные пересечения подмножеств вида: 
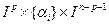называются кубиками. Кубики будут равны: 
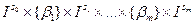, для некоторых 
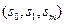и 
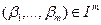, таких, что 
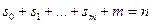. Если кубики являются максимальными, содержащимися в носителе, и попарно не пересекаются, то формула
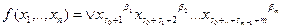
будет давать разложение в дизъюнктивную нормальную форму, минимальное по количеству слагаемых. Карты Карно позволяют «увидеть» эти кубики. Для функций двух, трех и четырех переменных они имеют следующие структуры:
|
x1 |
x2 |
0 |
1 |
|
0 |
f(0,0) |
f(0,1) |
|
|
1 |
f(1,0) |
f(1,1) |
|
|
x2 x3 |
00 |
01 |
11 |
10 |
|
|
x1 |
|||||
|
0 |
f(0,0,0) |
f(0,0,1) |
f(0,1,1) |
f(0,1,0) |
|
|
1 |
f(1,0,0) |
f(1,0,1) |
f(1,1,1) |
f(1,1,0) |
|
|
х3 x4 |
00 |
01 |
11 |
10 |
|
|
x1 x2 |
|||||
|
00 |
f(0,0,0,0) |
f(0,0,0,1) |
f(0,0,1,1) |
f(0,0,1,0) |
|
|
01 |
f(0,1,0,0) |
f(0,1,0,1) |
f(0,1,1,1) |
f(0,1,1,0) |
|
|
11 |
f(1,1,0,0) |
f(1,1,0,1) |
f(1,1,1,1) |
f(1,1,1,0) |
|
|
10 |
f(1,0,0,0) |
f(1,0,0,1) |
f(1,0,1,1) |
f(1,0,1,0) |
|
Кубикам будут соответствовать отрезки и квадраты. Рассмотрим примеры кубиков и соответствующих им логических произведений:
|
00 |
01 |
11 |
10 |
|
|
00 |
0 |
0 |
0 |
0 |
|
01 |
0 |
1 |
1 |
0 |
|
11 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
|
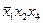
00 |
01 |
11 |
10 |
|
|
00 |
0 |
0 |
0 |
0 |
|
01 |
1 |
1 |
0 |
0 |
|
11 |
1 |
1 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
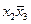
Возможно превращение кубиков в квадраты и отрезки после отождествления противоположных сторон карты Карно, например:
|
00 |
01 |
11 |
10 |
|
|
00 |
0 |
0 |
0 |
0 |
|
01 |
0 |
0 |
0 |
0 |
|
11 |
1 |
0 |
0 |
1 |
|
10 |
0 |
0 |
0 |
0 |
|
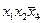
00 |
01 |
11 |
10 |
|
|
00 |
0 |
0 |
0 |
0 |
|
01 |
1 |
0 |
0 |
1 |
|
11 |
1 |
0 |
0 |
1 |
|
10 |
0 |
0 |
0 |
0 |
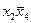
Логические произведения состоят из сомножителей, значения которых не изменяются внутри кубика.
Если это значение равно 1, то для переменной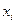 
берется сомножитель 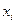, а если это значение равно 0 – то сомножитель 
.
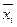Пример
Для булевой функции:
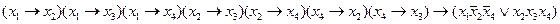
найти дизъюнктивную нормальную форму с наименьшим числом логических слагаемых.
Решение. Составим карту Карно:
|
|
х3 x4 |
00 |
01 |
11 |
10 |
|
x1 x2 |
|||||
|
00 |
1 |
0 |
0 |
1 |
|
|
01 |
0 |
0 |
1 |
0 |
|
|
11 |
0 |
0 |
1 |
0 |
|
|
10 |
1 |
0 |
0 |
1 |
|
Получаем 2 кубика: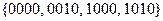 
и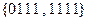 
. Внутри первого кубика не изменяются переменные 
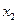и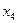 
, и равны 0. Значит, первое слагаемое равно: 
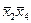. Внутри второго кубика не изменяются 
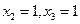и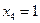 
, откуда второе слагаемое равно: 
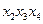. Следовательно, искомая дизъюнктивная нормальная форма равна: 
.
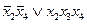