Теорема. Пусть функции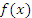 
и 
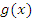непрерывны в замкнутом промежутке 
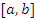; дифференцируемы в открытом промежутке 
; 
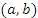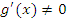в открытом промежутке 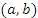. Тогда существует такая точка 
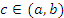, что
 |
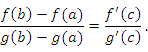(15) |
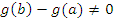. В противном случае – согласно теореме Ролля – производная 
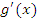обратилась бы в нуль в некоторой точке 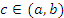. Рассмотрим вспомогательную функцию
:
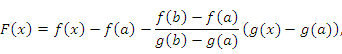
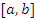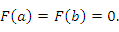
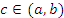, в которой
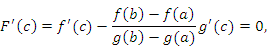что и требовалось доказать. 
