Точка 
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
- функция
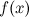определена в точке и ее окрестности; - существует конечный предел функции 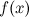в точке ;
- это предел равен значению функции в точке , т.е.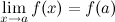
называется точкой разрыва функции.
Если в точке существуют конечные пределы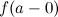 
и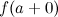 
, такие, что 
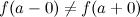, то точка называется точкой разрыва первого рода.
Если хотя б один из пределов 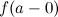или 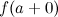не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции 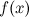в точке : 
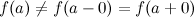или функция 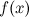не определена в точке , то точка называется точкой устранимого разрыва.
