Определение. Функция f(x) непрерывна в точке x0, если она определена в этой точке и некоторой ее окрестности и если
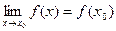
Свойства функций, непрерывных в точке:
1. Функция, непрерывная в точке, является ограниченной в некоторой окрестности этой точки.
2. Если функции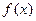 
и 
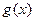непрерывны в некоторой точке 
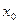, то непрерывными являются также функции:
;
;
;
, 
.
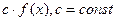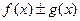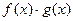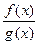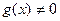3. Если функция 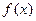непрерывна в точке 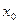и 
(
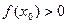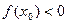), то существует некоторая окрестность точки 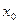, в которой 
(
).
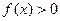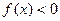4. Есл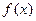и и 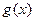непрерывны в некоторой точке 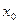и 
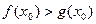, то существует некоторая окрестность точки 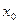, в которой 
.
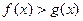5. Если функция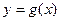 
непрерывна в точке 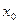, а функция 
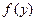непрерывна в точке 
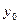, где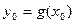 
, то сложная функция 
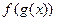непрерывна в точке .
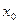6. Если для сложной функции выполняются условия ее непрерывности (5), то справедлива формула
.
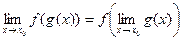