в квантовой механике.
Линейный гармонический осциллятор – это система, совершающая одномерное движение под действиемквазиупругой силы. Он является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна: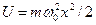
,(5.1)
где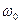 
— собственная частота колебаний осциллятора, т — масса частицы.
Рассмотрим сначала поведение классического гармонического осциллятора.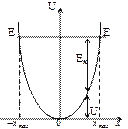 
Пусть частица с полной энергией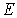 
совершает колебания в силовом поле (4.77)(рис.4.24). Точки 
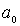и 
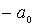, в которых полная энергия частицы равна потенциальной энергии 
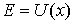, являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка 
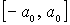, выйти за пределы которого она не может. Амплитуда колебаний 
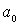определяется выражением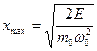 
.
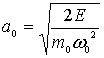Зависимость (5.1) имеет вид параболы (рис. 5.1), т.е. «потенциальная яма» в данном случае является параболической. Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е. В точках с координатами ±хmax полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (–хmax,+ хmax).
Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида
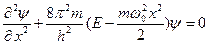(5.2)
где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что уравнение (5.2) решается только при собственных значениях энергии
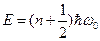(5.3)
где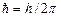 
. Формула (5.3)показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. квантуется.
Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии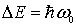 
друг от друга
Энергия ограничена снизу отличным от нуля минимальным значением энергии 
. Существование минимальной энергии, называемой энергией нулевых колебаний, представляет собой прямое следствие соотношения неопределенностей.
