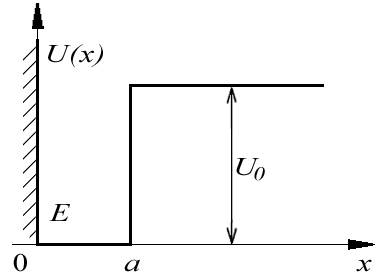
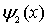а рассмотрим частицу в потенциальной яме с одной бесконечно высокой стенкой (рис.4.18).Птенциальная энергия двух частиц, между которыми действуют силы притяжения, например, двух атомов, образующих молекулу, по виду близка к рассматриваемой модели.
 |
|
Рис. 4.18.
|
Одномерная яма с одной бесконечно высокой стенкой. Рассмотрим частицу, движущуюся в одномерной потенциальной яме вида
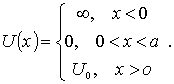
При 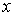 меньше 0 потенциальная энергия частицы бесконечна и волновая функция
меньше 0 потенциальная энергия частицы бесконечна и волновая функция 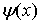 , как мы уже знаем, обращается в нуль. Поэтому уделим основное внимание при решении данной задачи исследованию движения частицы в области
, как мы уже знаем, обращается в нуль. Поэтому уделим основное внимание при решении данной задачи исследованию движения частицы в области 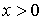 .
.
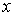 меньше 0 потенциальная энергия частицы бесконечна и волновая функция
меньше 0 потенциальная энергия частицы бесконечна и волновая функция 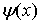 , как мы уже знаем, обращается в нуль. Поэтому уделим основное внимание при решении данной задачи исследованию движения частицы в области
, как мы уже знаем, обращается в нуль. Поэтому уделим основное внимание при решении данной задачи исследованию движения частицы в области 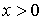 .
. Обозначим цифрой I область 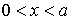 , а цифрой II - область
, а цифрой II - область 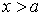 . Рассмотрим сначала случай, при котором полная энергия частицы
. Рассмотрим сначала случай, при котором полная энергия частицы 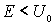 , т.е. будем считать, что частица находится в потенциальной яме. Уравнение Шредингера (4.6) в области I имеет вид
, т.е. будем считать, что частица находится в потенциальной яме. Уравнение Шредингера (4.6) в области I имеет вид
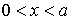 , а цифрой II - область
, а цифрой II - область 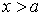 . Рассмотрим сначала случай, при котором полная энергия частицы
. Рассмотрим сначала случай, при котором полная энергия частицы 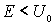 , т.е. будем считать, что частица находится в потенциальной яме. Уравнение Шредингера (4.6) в области I имеет вид
, т.е. будем считать, что частица находится в потенциальной яме. Уравнение Шредингера (4.6) в области I имеет вид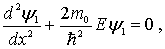 |
(4.56) |
а в области II
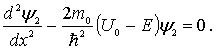 |
(4.57) |
Вводя обозначения
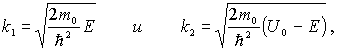 |
(4.58) |
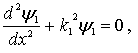 |
(4.59a) |
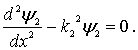 |
(4.59b) |
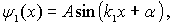 |
(4.60a) |
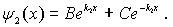 |
(4.60b) |
Воспользуемся условиями, налагаемыми на волновую функцию. Поскольку волновая функция должна быть всюду конечной, а первое слагаемое в (4.60b) при 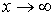 неограниченно возрастает, то необходимо потребовать, чтобы коэффициент
неограниченно возрастает, то необходимо потребовать, чтобы коэффициент 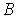 был равен нулю, т.е. чтобы
был равен нулю, т.е. чтобы 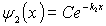 .
.
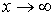 неограниченно возрастает, то необходимо потребовать, чтобы коэффициент
неограниченно возрастает, то необходимо потребовать, чтобы коэффициент 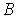 был равен нулю, т.е. чтобы
был равен нулю, т.е. чтобы 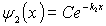 .
. Перейдем теперь к анализу граничных условий. Непрерывность волновой функции 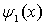 на левой границе ямы приводит, как мы уже видели в, к соотношению
на левой границе ямы приводит, как мы уже видели в, к соотношению 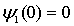 , откуда следует, что
, откуда следует, что 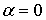 . Условие сшивки волновых функций и их производных при
. Условие сшивки волновых функций и их производных при 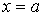 дает следующую систему уравнений
дает следующую систему уравнений
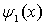 на левой границе ямы приводит, как мы уже видели в, к соотношению
на левой границе ямы приводит, как мы уже видели в, к соотношению 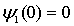 , откуда следует, что
, откуда следует, что 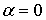 . Условие сшивки волновых функций и их производных при
. Условие сшивки волновых функций и их производных при 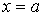 дает следующую систему уравнений
дает следующую систему уравнений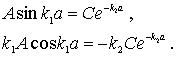 |
(4.61) |
Разделив первое уравнение (4.61) на второе, приходим к соотношению
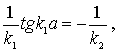 |
(4.62) |
которое и определяет энергетический спектр частицы в яме.
Ввиду того, что уравнение является трансцендентным, получить значения энергии частицы 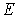 в явном виде не удается. Покажем с помощью графического метода, что энергетический спектр частицы, определяемый соотношением (4.62) с учетом (4.58) , является дискретным, т.е. энергия частицы в яме квантуется.
в явном виде не удается. Покажем с помощью графического метода, что энергетический спектр частицы, определяемый соотношением (4.62) с учетом (4.58) , является дискретным, т.е. энергия частицы в яме квантуется.
 в явном виде не удается. Покажем с помощью графического метода, что энергетический спектр частицы, определяемый соотношением (4.62) с учетом (4.58) , является дискретным, т.е. энергия частицы в яме квантуется.
в явном виде не удается. Покажем с помощью графического метода, что энергетический спектр частицы, определяемый соотношением (4.62) с учетом (4.58) , является дискретным, т.е. энергия частицы в яме квантуется. Уравнение (4.62) легко преобразуется к виду
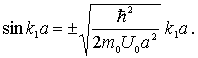 |
(4.63) |
Построим графики левой и правой частей уравнения (4.63) как функции параметра 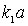 . Точки пересечения синусоиды с прямой (рис.4.19)
. Точки пересечения синусоиды с прямой (рис.4.19)
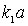 . Точки пересечения синусоиды с прямой (рис.4.19)
. Точки пересечения синусоиды с прямой (рис.4.19)
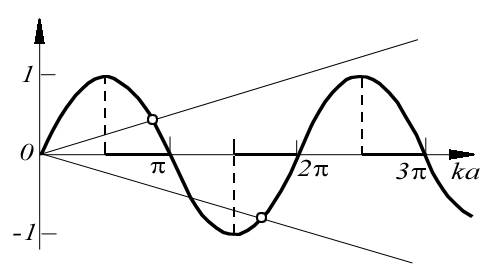 |
|
Рис. 4.19.
|
определяют корни уравнения (4.63) , отвечающие искомым значениям энергии частицы 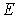 . Поскольку, согласно (4.62) ,
. Поскольку, согласно (4.62) , 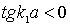 , то будем выбирать только те значения параметра
, то будем выбирать только те значения параметра 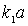 , которые удовлетворяют условию
, которые удовлетворяют условию
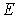 . Поскольку, согласно (4.62) ,
. Поскольку, согласно (4.62) , 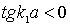 , то будем выбирать только те значения параметра
, то будем выбирать только те значения параметра 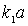 , которые удовлетворяют условию
, которые удовлетворяют условию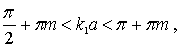
где 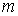 = 0, 1, 2, 3, ... На рис.4.19 соответствующие области значений
= 0, 1, 2, 3, ... На рис.4.19 соответствующие области значений 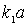 на оси абсцисс выделены жирной линией.
на оси абсцисс выделены жирной линией.
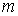 = 0, 1, 2, 3, ... На рис.4.19 соответствующие области значений
= 0, 1, 2, 3, ... На рис.4.19 соответствующие области значений 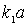 на оси абсцисс выделены жирной линией.
на оси абсцисс выделены жирной линией. Приведенные графики показывают, что энергетический спектр частицы является дискретным. Чем больше глубина 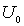 и ширина
и ширина 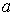 потенциальной ямы, тем ниже наклон прямой в правой части уравнения (4.63) и тем больше точек пересечения имеет прямая с синусоидой. Следовательно, тем больше энергетических уровней помещается в потенциальной яме.
потенциальной ямы, тем ниже наклон прямой в правой части уравнения (4.63) и тем больше точек пересечения имеет прямая с синусоидой. Следовательно, тем больше энергетических уровней помещается в потенциальной яме.
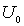 и ширина
и ширина 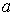 потенциальной ямы, тем ниже наклон прямой в правой части уравнения (4.63) и тем больше точек пересечения имеет прямая с синусоидой. Следовательно, тем больше энергетических уровней помещается в потенциальной яме.
потенциальной ямы, тем ниже наклон прямой в правой части уравнения (4.63) и тем больше точек пересечения имеет прямая с синусоидой. Следовательно, тем больше энергетических уровней помещается в потенциальной яме.

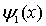 и
и