Согласно квантовой теории Планка, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями -- квантами, причем энергия ванта пропорциональна частоте колебания , где-- постоянная Планка. Т.к. излучение испускается порциями, то энергия осциллятора (стоячей волны)может принимать лишь определенные дискретные значения, кратные целому числу эл-тарн порций энергии: (n=0,1,2,…). Ф-ла Планка (нахождение универсальной функции Кирхгофа): 

, где, -- спектральные плотности энергетической светимости ЧТ, -- длина волны, -- круговая частота, с – скорость света в вакууме, к – постоянная Больцмана, Т – термодинамическая температура, h – постоянная Планка,  -- постоянная Планка, дел. на =. Следствие: если , то и из ф-лы Планка следует ф-ла Релея-Джинса:. В области больших частот и единицей в знаменателе ф-лы можно пренебречь по сравнению с, тогда получим ф-лу, эта ф-ла совпадает с ф-лой, причем а1=h/k

§20. Закон равномерного распределения энергии по степеням свободы.

Л. Больцман установил закон равномерного распределения энергии молекул идеального газа по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kT/2.

Таким образом, молекула с i-степенями свободы обладает средней кинетической энергией, равной

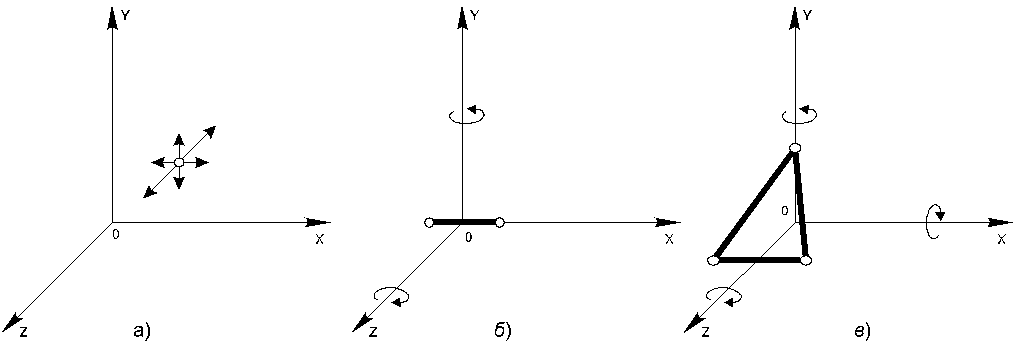
Рис.20.1

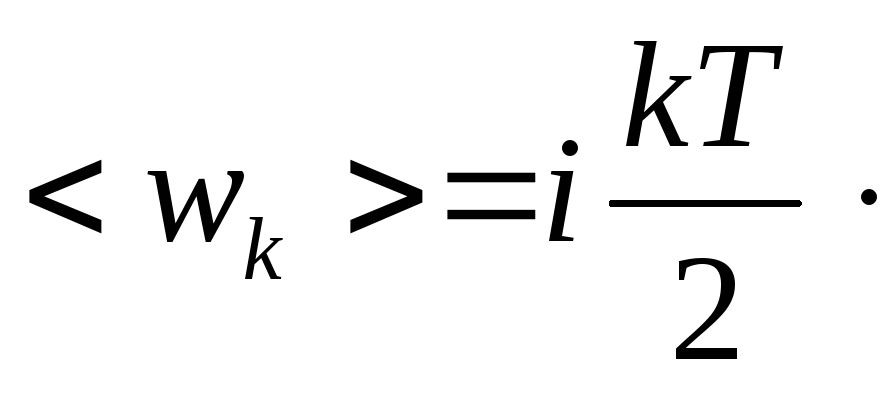(20.1)

 При определении числа степеней свободы молекул газов принимаются во внимание те степени свободы, которые вносят существенный вклад в ее кинетическую энергию.

Например, молекула одноатомного газа, принимаемая за материальную точку (рис.20.1.а) и способная совершать три независимых движениях (вдоль осей X, Y и Z), имеет три степени свободы. Следовательно, средняя кинетическая энергия такой молекулы 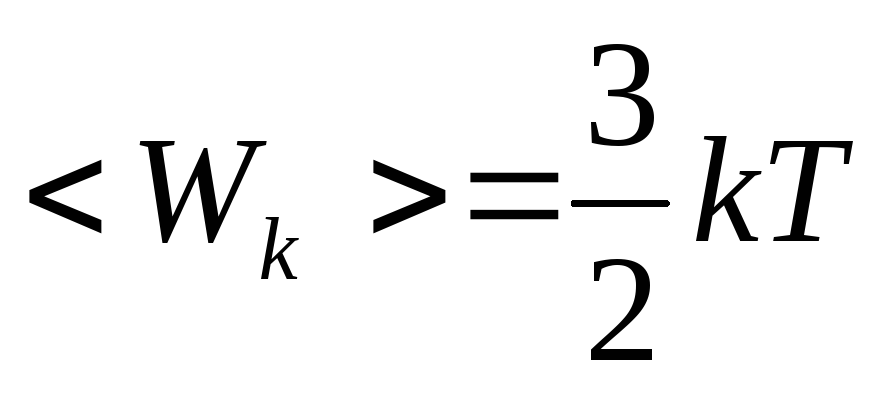. Ввиду хаотичности теплового движения молекул кинетическая энергия каждой из них равномерно распределяется между тремя степенями свободы, так что в среднем на каждую степень свободы приходится энергия, равнаяkT/2.

Молекулу двухатомного газа можно представить в виде двух атомов, жестко связанных друг с другом (рис.20.1.б). Кроме трех степеней свободы поступательного движения, такая система имеет еще две степени свободы вращения вокруг осей Y и Z  Таким образом, двухатомная молекула имеет пять степеней свободы и, следовательно, обладает средней кинетической энергией .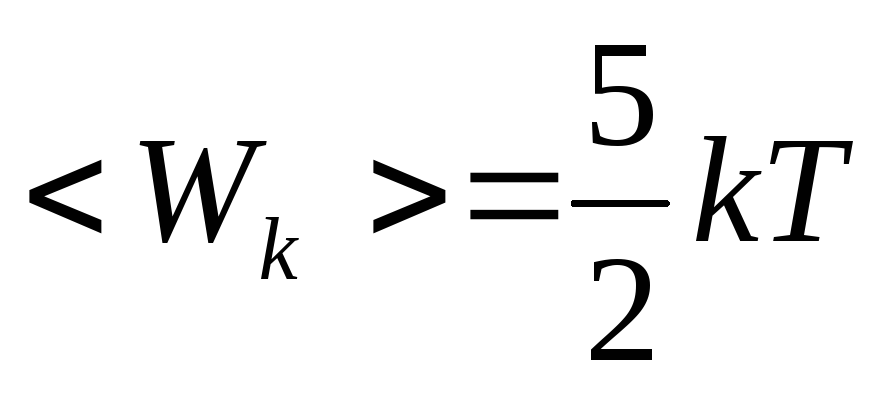

Молекулы, состоящие из трех и более атомов, имеют шесть степеней свободы: три поступательных и три вращательных (рис.20.1.в). Для таких молекул .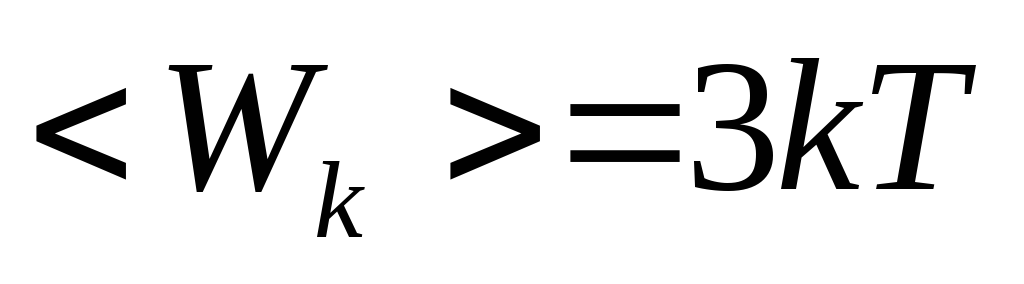

Строго говоря, связи между атомами в молекулах реальных газов не являются абсолютно жесткими, поэтому при некоторых условиях (например, при повышенных температурах) эти связи скорее можно представить в виде упругих пружин, результатом чего являются дополнительные, колебательные степени свободы.

Закон равномерного распределения энергии по степеням свободы приводит к выводу о равноправности всех степеней свободы молекулы: все они вносят одинаковый вклад в ее среднюю кинетическую энергию.Однако этот вывод имеет ограниченную область применимости и уточнен в квантовой статистике.