Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
|
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l.
| B = μ0 I n, |
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.
Магнитный поток, пронизывающий все N витков соленоида, равен
| Φ = B S N = μ0 n2 S l I. |
Следовательно, индуктивность соленоида равна
|
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз (см. § 1.17); поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
|
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна
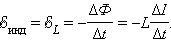 |
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

