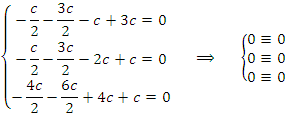Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:
Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение.
Пример
Решить однородную систему линейных уравнений
Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.
(2) К третьей строке прибавили вторую строку, умноженную на –1.
Делить третью строку на 3 не имеет особого смысла.
В результате элементарных преобразований получена эквивалентная однородная система , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
Ответ:
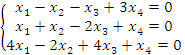
методом Гаусса.
Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
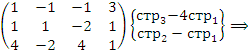
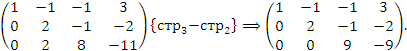
Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,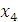 
следует рассматривать как свободный параметр.
Далее нужно присвоить этому параметру произвольное значение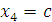 
и выразить базисные неизвестные 
, 
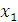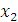и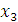 
через c.
Преобразованная матрица соответствует следующей системе уравнений:
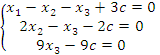
Из последнего уравнения следует, что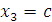 
.
Выразим остальные базисные переменные:
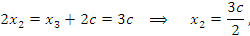
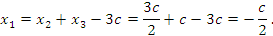
Таким образом, общее решение системы найдено:
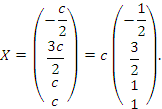
Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
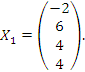
Проверка: Подставим неизвестные
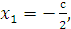
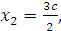
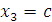
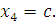
в уравнения системы:
