Функция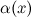 
называется бесконечно малой функцией (б.м.ф.) при 
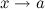(или в точке 
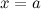), если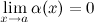 
Функция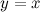 
является бесконечно малой (б.м) функцией при 
.
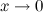Основные свойства бесконечно малых функций
1° Сумма конечного числа б.м функций является функцией б.м.
2° Произведение б.м функции на ограниченную есть функция б.м.
3° Произведение двух б.м функций есть функция б.м.
4° Произведение б.м функции на константу является б.м функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6° Функция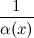 
, обратная к б.м функции 
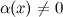, есть функция бесконечно большая. Верно и обратное
Доказать, что функция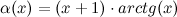 
является бесконечно малой в точке 
.
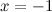Доказательство. Из того, что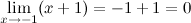 
делаем вывод, что функция 
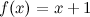является б.м при 
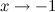. Функция 
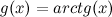является ограниченной: 
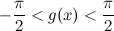. А тогда их произведение 
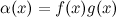, согласно свойству №3, является функцией б.м.
Б.м. функции 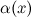и 
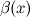называются эквивалентными или равносильными б.м. одного порядка при 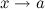, если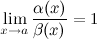 
Обозначают: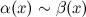 
при .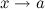
Проверить, являются ли функци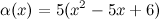и 
и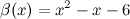 
эквивалентными бесконечно малыми при 
.
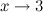Решение. Проверим вначале, что данные функции являются бесконечно малыми функциями в точке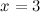 
:
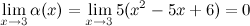
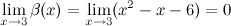
Найдем предел отношения этих функций:
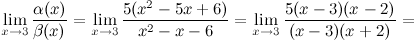
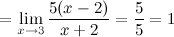
Ответ. Заданные функци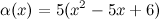и и 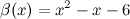являются эквивалентными бесконечно малыми.
