Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
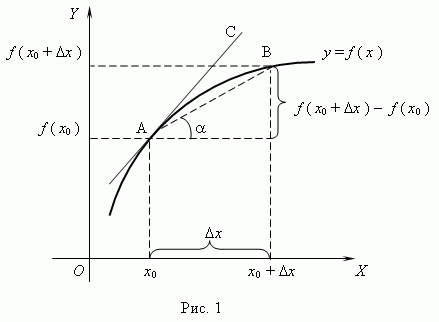
Из рис.1 видно, что для любых двух точек A и B графика функции:
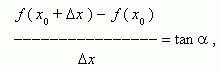
где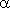 
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то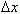 
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Определение производной функции в точке.
Пусть функция f(x) определена на промежутке (a; b), 
и 
- точки этого промежутка. Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при 
. Обозначается 
.
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.
Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.
Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке 
, то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x) на интервале (a; b).
