32.Определение комплексных чисел.действия над ними

Комплексным числом называется выражение вида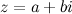

Действительное число называется действительной частью комплексного числа 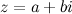и обозначается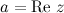

Действительное число 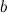называется мнимой частью числа 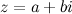и обозначается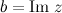

Для комплексного числа 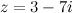действительная часть 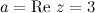, а мнимая - .

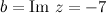Если действительная часть комплексного числа 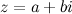равна нулю ( 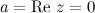), то комплексное число называется чисто мнимым.(. )

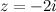Действия

1. Коммутативность сложения:

   z1 + z2 = z2 + z1

   для любых   .
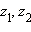
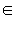
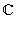2. Ассоциативность сложения:

   (z1 + z2) + z3 = z1 + (z2 + z3)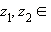

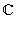   для любых .
3. Существует такое число z = 0, которое обладает свойством

   z + 0 = z

   для любого z  .
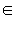
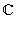4. Для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.
5. Коммутативность умножения:

   z1z2 = z2z1

   для любых   .
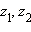
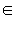
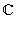6. Ассоциативность умножения:

   (z1z2)z3 = z1(z2z3)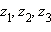

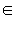
   для любых   .
7. Дистрибутивность сложения относительно умножения:

   z1(z2 + z3) = z1z2 + z1z3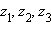

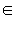
   для любых   .
8. Для любого комплексного числа z:

   z · 1 = z.

9. Для любых двух чисел 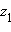и 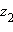существует такое число z, что 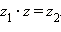Такое число z называется частным двух комплексных чисел и обозначается 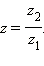Деление на 0 невозможно.