30.Метод Крамера решения систем уравнений

Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

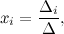
где 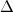- определитель матрицы системы, 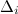- определитель матрицы системы, где вместо 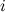-го столбца стоит столбец правых частей.

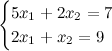при помощи метода Крамера.

Решение. Вычисляем определитель матрицы системы:

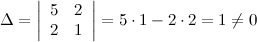
Так как 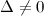, то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель 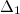получим из определителя 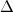заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:

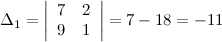
Аналогично, определитель 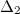получается из определителя матрицы системы 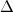заменой второго столбца столбцом свободных коэффициентов:

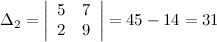
Тогда получаем, что

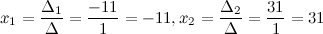
Ответ. ,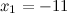

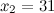
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.

1. Вычисляем определитель основной матрицы системы  и убеждаемся, что он отличен от нуля.
2. Находим определители
    
   которые являются определителями матриц, полученных из матрицы А заменой k-огостолбца (k = 1, 2, …, n) на столбец свободных членов.
3. Вычисляем искомые неизвестные переменные x₁, x₂, …, x_n по формулам .
4. Выполняем проверку результатов, подставляя x₁, x₂, …, x_n в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.

5. Выполним проверку. Подставим полученные значения x₁ и x₂ в исходную систему уравнений:
   

   Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.