Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
Решить систему уравнений методом обратной матрицы.
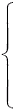 |
2 x1 | + | 3 x2 | = | 4 | |
| - 2 x1 | + | x2 | = | 5 |
Решение:
Введем обозначения:
| A = |  |
2 | 3 |  |
- матрица А состоит из коэффициентов системы. |
| -2 | 1 |
| X = |  |
x 1 |  |
- матрица X состоит из переменных, которые необходимо найти. |
| x 2 |
| B = |  |
4 |  |
- матрица B состоит из столбца свободных членов. |
| 5 |
| E = |  |
1 | 0 |  |
- единичная матрица. |
| 0 | 1 |
Теперь исходную систему уравнений можно записать в виде матричного уравнения.
A * X = B
Необходимо найти матрицу X.
Умножим (слева) левую и правую часть уравнения на A-1 - матрицу обратную матрице A.
A -1 * A * X = A -1 * B
Согласно определению обратной матрицы: A -1 * A = E
E * X = A -1 * B
Согласно определению единичной матрицы: E * X = X
X = A -1 * B
Вывод: задача сводится к нахождению обратной матрицы A -1
|
* |
|
| X = A -1 * B = 1 / 8 * |  |
-11 |  |
| 18 |
| X = |  |
-11/8 |  |
| 9/4 |
Ответ:
x1 = -11/8
x2 = 9/4

