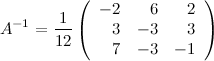Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E
Нахождение
1.Дописание к квадратной матрице справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.
2.для матрицы второго порядка
Шаг 1. Находим определитель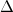 
заданной матрицы, если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.
Шаг 2. Элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный.
Шаг 3. Делим все элементы на 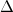и получаем обратную матрицу.
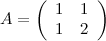
Решение. Шаг 1. Находим определитель: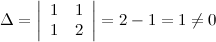 
Шаг 2.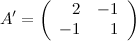 
Шаг 3.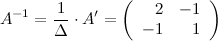 
Ответ.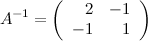 
3.Нахождение обратной матрицы с помощью союзной матрицы
Найти обратную матрицу к матрице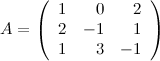 
Решение. Вычисляем определитель матрицы:
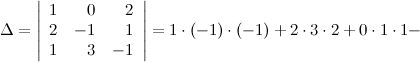
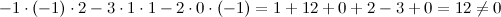
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица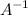 
к матрице 
находится по формуле:
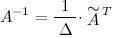
Найдем союзную матрицу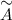 
, для этого вычислим алгебраические дополнения к элементам матрицы :
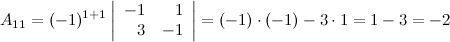
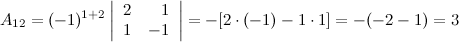
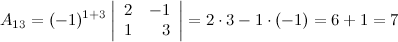
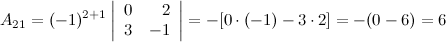
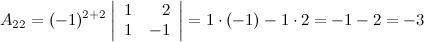
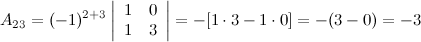
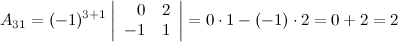
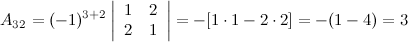
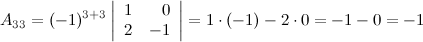
Таким образом,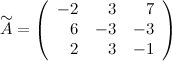 
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
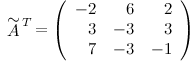
Итак,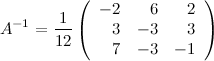 
Ответ.
