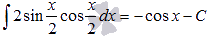17.Определение первообразной функции и неопределенный интеграл

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 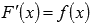для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 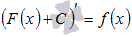. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Пример

Найти первообразную функции , значение которой равно единице при х = 1.

Мы знаем из дифференциального исчисления, что 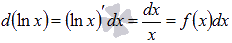(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, 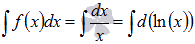. По второму свойству 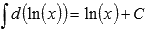. То есть, имеем множество первообразных 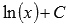. При х = 1 получим значение 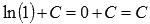. По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид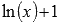

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .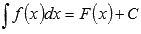

Выражение 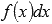называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

Пример

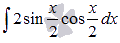
По формуле синуса двойного угла из тригонометрии 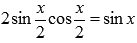, поэтому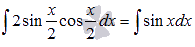

Из таблицы производных для тригонометрических функций имеем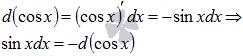

То есть,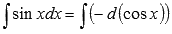

По третьему свойству неопределенного интеграла можем записать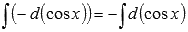

Обращаясь ко второму свойству, получим .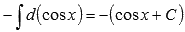

Следовательно,