- Область определения
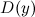и область допустимых значений 
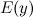функции. - Четность, нечетность функции.
- Точки пересечения с осями.
- Асимптоты функции.
- Экстремумы и интервалы монотонности.
- Точки перегиба и промежутки выпуклости, вогнутости.
- Сводная таблица.
1. Находим область определения (D(f)) функции 
.
2. Если область определения функции симметрична относительно нуля (то есть для любого значения 
из D(f) значение 
также принадлежит области определения, то проверяем функцию на четность.
Если 
, то функция четная. (Примером четной функции является функция 
)
Для нас важно, что график четной функции симметричен относительно оси OY.
Если 
, то функция нечетная. (Примером нечетной функции является функция 
)
График нечетной функции симметричен относительно начала координат.
Если функция является четной или нечетной, то мы можем построить часть ее графика для 
, а затем соответствующим образом отразить ее.
3. Находим точки пересечения графика с осями координат.
Находим нули функции - это точки пересечения графика функции с осью абсцисс (OX).
Для этого мы решаем уравнение 
.
Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.
Находим точку пересечения графика функции с осью ординат (OY). Для этого ищем значение функции при 
.
4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции , нам нужно решить неравенства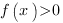 
и 
.
5. Находим асимптоты графика функции.
6. Если функция периодическая, то находим период функции.
7. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную 
б) Приравниваем производную к нулю и находим корни уравнения 
- это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
8. И последний номер наше программы - точки перегибы и промежутки выпуклости и вогнутости.
https://www.kontrolnaya-rabota.ru/s/grafik/xy/
