15. Понятие экстремума.Необходимое и достаточное условие экстремума.Примеры

Точку формула называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают формула .

Точку формула называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают формула .

Под окрестностью точки формула понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

(Необходимое условие экстремума)

Если функция имеет экстремум в точке 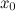, то ее производная 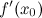либо равна нулю, либо не существует.

Не путайте экстремумы функции с наибольшим и наименьшим значением функции.

На первом рисунке наибольшее значение функции на отрезке [a;b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b, которая не является точкой максимума.

(Необходимое условие экстремума)

Если функция имеет экстремум в точке 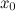, то ее производная 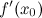либо равна нулю, либо не существует.

(Достаточное условие экстремума)

а) Пусть функция дифференцируема в некоторой окрестности U точки х0, не содержащей других критических точек. Тогда:

если при переходе через точку х0 производная f ' меняет свой знак с плюса на минус, х0 – точка (локального) максимума функции;
если при переходе через точку х0 производная меняет свой знак с минуса на плюс, х0 – точка (локального) минимума функции;
если при переходе через точку х0 производная не меняет свой знак, в точке х0 нет экстремума.

б) Пусть в точке х0 существует вторая производная функции f, f ''(x0), не равная нулю. Тогда:
если f’’(x0) > 0, х0 – точка (локального) минимума функции;