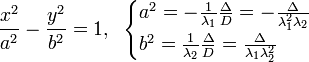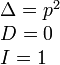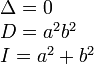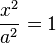Вводя новую систему координат можно привести уравнения кривых второго порядка к стандартному
каноническому виду. Характеристики канонических уравнений очень легко выражаются через инварианты
Δ, D, I и корни характеристического уравнения  .
.
|
Вид кривой |
Каноническое уравнение |
Инварианты |
| Невырожденные кривые (Δ ≠ 0) | ||
|
Эллипс |
|
|
|
Гипербола |
|
|
|
Парабола |
|
|
| Вырожденные кривые (Δ = 0) | ||
|
Точка |
|
|
|
Две пересекающиеся прямые |
|
|
|
Две параллельные прямые |
|
|
|
Одна прямая |
|
|
|
Для центральной кривой в каноническом виде её центр (x0, y0) находится в начале координат. |