признак сходимости Дирихле:  1. пусть функция f(x) интегрируема в любом конечном промежутке [a, b], и интеграл по этому промежутку ограничен (как функция верхнего предела b):
1. пусть функция f(x) интегрируема в любом конечном промежутке [a, b], и интеграл по этому промежутку ограничен (как функция верхнего предела b): ;
;  2. g(x) монотонно стремится к нулю при
2. g(x) монотонно стремится к нулю при  :
:  .
.
Тогда интеграл  сходится.
сходится.  Применим, например, признак Дирихле к
Применим, например, признак Дирихле к  . Здесь f(x) = cos x, g(x) = 1/x, условия признака выполнены, поэтому интеграл сходится условно.
. Здесь f(x) = cos x, g(x) = 1/x, условия признака выполнены, поэтому интеграл сходится условно.
Несобственный интеграл первого рода
Таким образом, по определению
Если такой предел существует, то говорят, что несобственный интеграл сходится. В противном случае, если предел не существует или бесконечен, то несобственный интеграл является расходящимся.
Аналогичным образом задается несобственный интеграл на промежутке .
Несобственный интеграл первого рода с двумя бесконечными пределами определяется формулой:
Такой несобственный интеграл сходится только в том случае, когда оба несобственных интеграла в правой части являютсясходящимися.
| Задание | Вычислить несобственный интеграл или установить его расходимость.
|
| Решение | Заданный интеграл является несобственным интегралом первого рода, так как на промежутке интегрирования |
| Ответ | 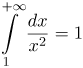 |

