Несобственные интегралы по бесконечному промежутку.
Рассмотрим функцию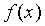 
определенную и непрерывную на промежутке 
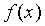. Очевидно, определение определенного интеграла на таком промежутке бессмысленно. Предположим, что данная функция интегрируема на любом конечном промежутке вида [a, A]. Тогда интегралом от этой функции по бесконечному промежутку назовем 
. Обозначать этот интеграл будем как 
. Таким образом
= (1)
Если этот предел существует, будем говорить, что интеграл сходится, в противном случае - расходится.
Геометрически этот интеграл представляет собой площадь бесконечной фигуры.
Аналогично можно определить интегралы по промежуткам другого вида
(2)
или
(3)
http://de.ifmo.ru/bk_netra/page.php?index=22&layer=2&tutindex=21
