В некоторых приложениях несобственных интегралов возникает необходимость использования углубленного понятия сходимости. (Одно из таких приложений рассматривается в разделе "Интегралы, зависящие от параметра".) С этой целью рассмотрим следующие возможные случаи.
- Пусть функция f(x) интегрируема на полубесконечном интервале [A, ∞). Если наряду с интегралом
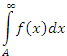сходится и интеграл 
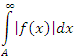, то интеграл 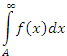называется абсолютно сходящимся. Говорят также, что функция f(x) абсолютно интегрируема на промежутке [A, ∞). - Если интеграл 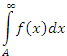сходится, тогда как интеграл 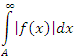расходится, то интеграл 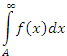называется условно сходящимся.
Заметим, что из сходимости интеграла 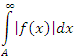вытекает сходимость интеграла 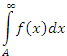, тогда как обратное утверждение является несправедливым.
Приведем полезные свойства абсолютно интегрируемых функций, доказательство которого предоставляется читателю.
- Пусть функция f(x) абсолютно интегрируема на промежутке [A, ∞). Если функция g(x) ограничена на этом промежутке, то и произведение
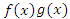является абсолютно интегрируемой функцией на промежутке [A, ∞). - Если функция f(x) абсолютно интегрируема на промежутке [A, ∞) и | g(x) | ≤ | f(x) |, то и функция g(x) абсолютно интегрируема на промежутке [A, ∞).
