{Определение тела вращения и его объема}

Тела вращения – это объемные тела, которые образуются при вращении некой плоской фигуры, которая, в свою очередь, ограничена кривой и вращается вокруг оси, лежащей в той же плоскости.

Определение кубируемости

Тело $M$ – называется кубируемым, если верхний объем $\overline{V}$ совпадает с нижним $\underline{V}$ и тогда величина $V=\overline{V}=\underline{V}$ называется объемом $M$ .

Пусть Тело $M$ – тело вращения, полученное вращением некоторой плоской фигуры вокруг оси $OX$ или $OY$ .
$M$ – кубируемо и его объем вычисляется по формуле $V=\pi\int\limits_{a}^{b} f^2(x) dx$ .
Вот пример тела полученого вращением вокруг оси $OX$ криволинейной трапеции, образованной непрерывной функцией $y=f(x)$ и прямыми $x=a$ и $x=b$ .

матхелп http://mathhelpplanet.com/static.php?p=vychislenie-obemov-tel-s-pomoshchyu-integralov

Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси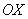

Пример 1

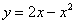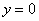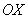Вычислить объем тела, полученного вращением фигуры, ограниченной линиями , вокруг оси obyem_tela_vrashenija_clip_image002_0001 .

Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости 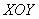необходимо построить фигуру, ограниченную линиями 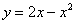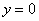obyem_tela_vrashenija_clip_image006_0000 , , при этом не забываем, что уравнение 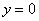задаёт ось 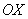. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницах Графики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.

Чертёж здесь довольно прост:

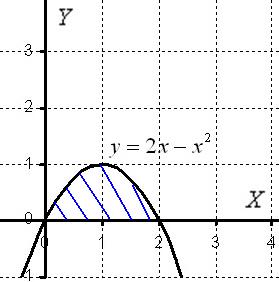
Объем тела, образованного вращением плоской фигуры, вокруг оси OX

Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси 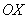obyem_tela_vrashenija_clip_image002_0003 В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси 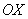. На самом деле у тела есть математическое название, но по справочнику что-то лень уточнять, поэтому едем дальше.

Как вычислить объем тела вращения?

Объем тела вращения можно вычислить по формуле:

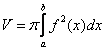
В формуле перед интегралом обязательно присутствует число 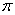. Так повелось – всё, что в жизни крутится, связано с этой константой.

Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.

Функция 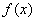… что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы 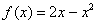сверху. Это и есть та функция, которая подразумевается в формуле.

В практических заданиях плоская фигура иногда может располагаться и ниже оси 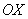obyem_tela_vrashenija_clip_image002_0005 . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат: 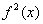, таким образом интеграл всегда неотрицателен, что весьма логично.

Вычислим объем тела вращения, используя данную формулу: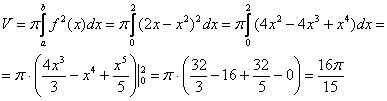

Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.

Ответ: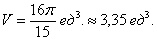

В ответе нужно обязательно указать размерность – кубические единицы 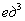. То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.

матпрофи http://mathprofi.ru/obyem_tela_vrashenija.html

Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси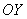

Второй параграф будет еще интереснее, чем первый. Задание на вычисление объема тела вращения вокруг оси ординат – тоже достаточно частый гость в контрольных работах. Попутно будет рассмотрена задача о нахождении площади фигуры вторым способом – интегрированием по оси 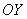obyem_tela_vrashenija_clip_image004_0003 , это позволит вам не только улучшить свои навыки, но и научит находить наиболее выгодный путь решения. В этом есть и практический жизненный смысл! Как с улыбкой вспоминала мой преподаватель по методике преподавания математики, многие выпускники благодарили её словами: «Нам очень помог Ваш предмет, теперь мы эффективные менеджеры и оптимально руководим персоналом». Пользуясь случаем, я тоже выражаю ей свою большую благодарность, тем более, что использую полученные знания по прямому назначению =).

Рекомендую для прочтения всем, даже полным чайникам. Более того, усвоенный материал второго параграфа окажет неоценимую помощь при вычислении двойных интегралов. (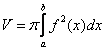 Вместо (x) ставит (y)

Определение тела вращения и его объема

{Определение тела вращения и его объема}

Определение кубируемости

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси

Как вычислить объем тела вращения?

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси

Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси

Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси