Вычисление длины дуги в случае параметрического задания кривой.
Если кривая (в пространстве или на плоскости) задана параметрическими уравнениями: x = x(t), y = y(t), z = z(t), где функции x(t), y(t), z(t) заданы, непрерывны и непрерывно дифференцируемы на промежутке [a, в], то длина дуги равна
(1)
для пространственной кривой и
(2)
для кривой, лежащей в плоскости OXY. Примеры
Матпрофи решения http://mathprofi.ru/dlina_dugi_krivoi.html
Как найти длину дуги кривой, если линия задана параметрически?
Если линия задана параметрическими уравнениями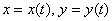 
, то при выполнении некоторых условий, на которых я не буду останавливаться, длина дуги кривой 
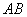, которая прочерчивается при изменении параметра в пределах 
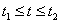, рассчитывается по формуле:
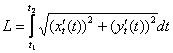, где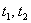 
– значения, определяющие точк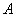и 
и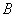 
.
В начале урока о площади и объёме при линиях, заданных параметрически, я обратил ваше внимание на тот факт, что параметрические уравнения могут «прорисовывать» кривую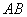 
как слева направо, так и справа налево, из-за чего во втором случае «вылезает минус» и возникают небольшие технические затруднения. В рассматриваемой задаче мы от этого избавлены! Так как подынтегральная функция, как и в первом пункте, неотрицательна 
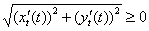, то заранее можно утверждать, что результата со знаком «минус» получиться не должно (понятно, при условии 
).
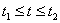Однако вместо «вопроса прорисовки дуги» у нас появляется другая почётная обязанность – беречь неотрицательность подынтегральной функции, как зеницу ока:
