Предположим, что функциональная зависимость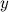 
от 
не задана непосредственно 
, а через промежуточную величину —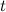 
. Тогда формулы
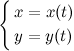
задают параметрическое представление функции одной переменной.
Пусть функция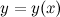 
задана в параметрической форме, то есть в виде:
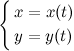
где функци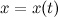и 
и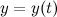 
определены и непрерывны на некотором интервале изменения параметра 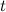. Найдем дифференциалы от правых и левых частей каждого из равенств:
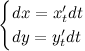
Далее, разделив второе уравнение на первое, и с учетом того, что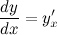 
, получим выражение для первой производной функции, заданной параметрически:
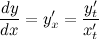
Для нахождения второй производной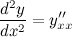 
выполним следующие преобразования:
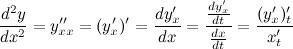
Примеры http://www.webmath.ru/primeri_reshenii/derivative.php?part=11&example=1
Параметрическое задание кривой или поверхности имеет известные преимущества над другими методами, в частности, потому, что оно не накладывает практически никаких ограничений на множество вершин в опорном массиве
