Интеграл с переменным верхним пределом
Пусть на отрезке [ a, b ] задана непрерывная функция f ( x ), тогда для любого x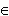 
[ a, b ] существует функция:
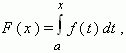
задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
| П р и м е р . | Переменная сила на прямолинейном пути изменяется по закону: f ( x ) = 6x2 + 5 при x 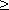 0. По какому закону изменяется работа этой силы ? |
| Р е ш е н и е. | Работа силы f ( x ) на отрезке [ 0 , x ] прямолинейного пути равна: 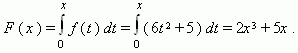 Таким образом, работа изменяется по закону: F ( x ) = 2x 3 + 5x . |
Из определения интеграла с переменным верхним пределом - функции F(x) и известных свойств интеграла следует, что при x 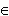[ a, b ]
F' ( x ) = f ( x ) .
