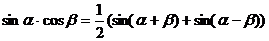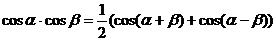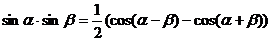Интегрирование выражений вида R(Sin(x)),Cos(x)

Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку, которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

1. Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x) = t и тогда sin(x)dx = -dt.
2. При R(sin(x),-cosx) = - R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
3. В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t), , или замену ctg(x)=t, если это удобнее

4. Интегрирование функций рационально зависящих от тригонометрических функций

   1. Интегралы вида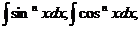 n>0 
   a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции. 
   б) Если n чётное, то пользуемся формулами понижения степени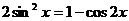 
   , . 
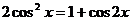   2. Интегралы вида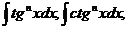  где n – целое. 
   Необходимо использовать формулы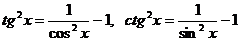 
    
   3. Интегралы вида 
   а) Пусть m и n разной чётности. Применяем подстановку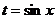 , если n - нечётное либо 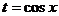, если m – нечётное. 
   б) Если m и n чётные, то пользуемся формулами понижения степени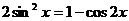 
   , . 
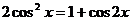   4. Интегралы вида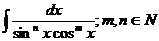  
   Если числа m и n одинаковой чётности, то используем подстановку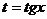 . Часто бывает удобным применить приём тригонометрической единицы. 
   5.  
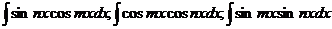
   Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму