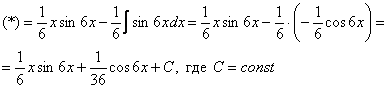Пример 1
Найти неопределенный интеграл.
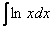
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
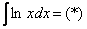
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям: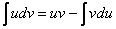 
Формула применяется слева направо
Смотрим на левую часть: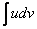 
. Очевидно, что в нашем примере 
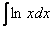(и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за 
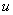, а что-то за 
.
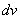В интегралах рассматриваемого типа за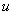 
всегда обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
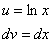
То есть, за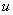 
мы обозначили логарифм, а за 
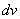– оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал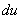 
:
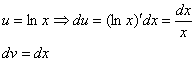
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию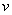 
. Для того чтобы найти функцию 
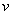необходимо проинтегрировать правую часть нижнего равенства 
:
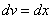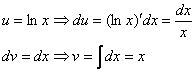
Теперь открываем наше решение и конструируем правую часть формулы: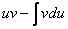 
.
Вот кстати, и образец чистового решения с небольшими пометками:
Единственный момент, в произведении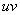 
я сразу переставил местам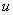и 
и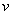 
, так как множитель 
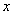принято записывать перед логарифмом.
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
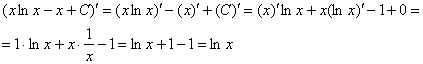
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения: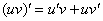 
. И это не случайно.
Формула интегрирования по частям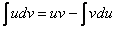 
и формула 
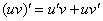– это два взаимно обратных правила.
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за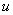 
всегда обозначается многочлен
Пример 5
Найти неопределенный интеграл.
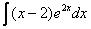
Решение:
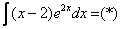
Используя знакомый алгоритм, интегрируем по частям:
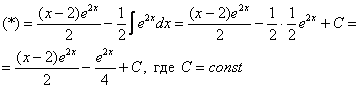
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за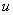 
всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
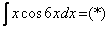
Интегрируем по частям:
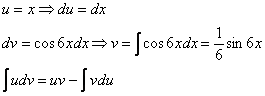
Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за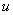 
всегда обозначается обратная тригонометрическая функция.
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
Пример 11
Найти неопределенный интеграл.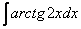
Решаем.
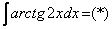
Интегрируем по частям: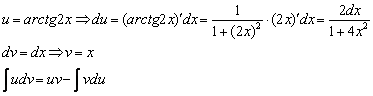
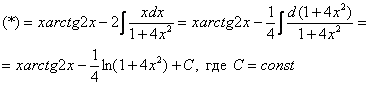
Интеграл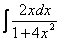 
найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.
Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
