Случай независимой переменной
Пусть 
- функция независимой переменной 
, имеющая дифференциалы любого порядка. Первый дифференциал функции
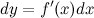
где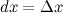 
- некоторое приращение независимой переменной , которое мы задаем сами и которое не зависит от .
По определению
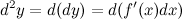
Переменной является аргумент . Значит, для дифференциала величина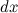 
является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
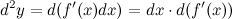
Для вычисления дифференциала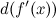 
применим формулу дифференциала первого порядка к функции 
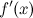. Тогда получим:
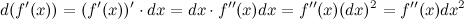
Итак,
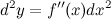
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала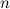 
-го порядка:
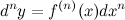
Задание. Найти дифференциал третьего порядка функции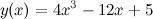 
Решение. По формуле
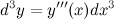
Найдем третью производную заданной функции:
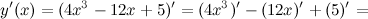
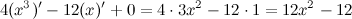
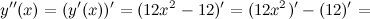
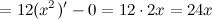
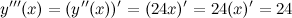
Тогда
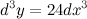
Ответ.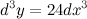
http://www.webmath.ru/primeri_reshenii/derivative.php?part=9&example=1 <<<пример
http://www.webmath.ru/poleznoe/formules_8_13.php <<вообще
