Рассмотрим многочлен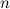 
-й степени
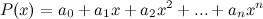
Его можно представить в виде суммы степеней 
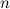, взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке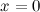 
:
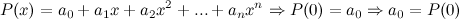
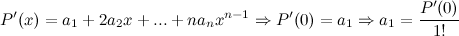
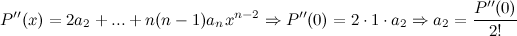
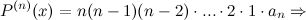
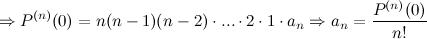
Таким образом, получаем, что
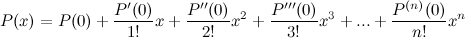
Полученное выражение называется формулой Маклорена для многочлена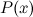 
степени .
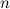Рассуждая аналогично, можно разложить многочлен 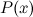по степеням разности 
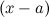, где 
- любое число. В этом случае будем иметь:
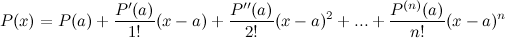
Это выражение называется формулой Тейлора для многочлена 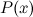в окрестности точки .
Пример:
Задание. Разложить в ряд Тейлора функцию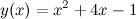 
в точке 
.
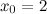Решение. Найдем производные:
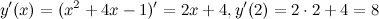
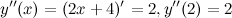
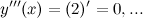
Итак,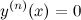 
, 
, 
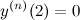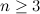. Значение функции в точке
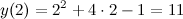
Таким образом,
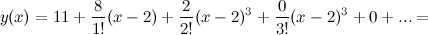
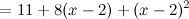
Ответ.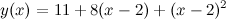 
ссылка: http://www.webmath.ru/primeri_reshenii/derivative.php?part=13&example=1
