Определение 4. Функция f называется эквивалентной функции g (или асимптотически равной ей) при
x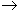 x0, если
x0, если
|
|
В этом случае пишут
f ~ g, x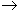 x0
x0
Пусть x → 0. Тогда справедливы следующие соотношения эквивалентности бесконечно малых функций.
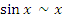 |
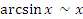 |
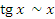 |
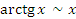 |
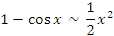 |
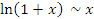 |
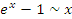 |
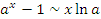 |
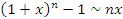 |
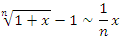 |
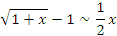 |
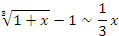 |
Приведенная таблица допускает более широкое толкование, а именно: если 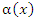 – бесконечно малая функция при x → a, то
– бесконечно малая функция при x → a, то
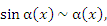
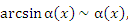
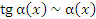
Определение :
Если в которой определены
и
,
причём и
– эквивалентные при
и пишут
Понятие эквивалентные обычно используют, когда f и g –бесконечно малые или бесконечно большие при
Критерий:
Для того, чтобы две бесконечно малые и
были эквивалентны, необходимо и достаточно, чтобы было
Положив , будем иметь
Отсюда сразу и вытекает наше утверждение. Действительно, если , то
, то есть
есть бесконечно малая высшего порядка, чем
и
. Обратно, если дано, что
, то
, а тогда
.
С помощью этого критерия, например, видно, что при бесконечно малая
эквивалентна
, а
.
Доказанное свойство эквивалентных бесконечно малых приводит к использованию их при раскрытии неопределённости . Т.е. при разыскании предела отношения двух бесконечно малых
. Каждая из них при этом может быть заменена, без влияния на предел, любой эквивалентной ей бесконечно малой.
ПРИМЕР:
3) Найдем  [ln(1 + x)/sin 2x]. Поскольку
[ln(1 + x)/sin 2x]. Поскольку
ln(1 + x) ~ x, sin 2x ~ 2x, x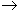 0,
0,
то
 [ln(1 + x)/sin 2x] =
[ln(1 + x)/sin 2x] =  x/2x = 1/2.
x/2x = 1/2.
1)
2)


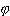 (x) = 1.
(x) = 1.