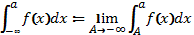Означення: Нехай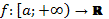 
, f інтегрована на 
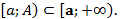Якщо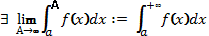 
, то ця границя називається невласним інтегралом 1-го роду від функції f на проміжку [
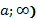. У цьому випадку f називають інтегрованою у невласному сенсі.
Якщо вказана в означенні границя існує, то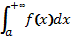 
називається збіжним, якщо границя не існує, то 
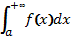називається розбіжним.
Означення: Нехай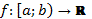 
, f інтегрована на 
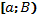, що міститься в [a;b). Якщо 
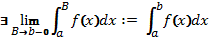, то ця границя називається невласним інтегралом 2-го роду за проміжком [a;b), функцію f можна називати інтегрованою у невласному сенсі.
Якщо вказана в означенні границя існує, то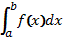 
називається збіжним, якщо границя не існує, то 
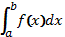називається розбіжним.
Зауваження! Так само, як ми розглядали за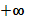 
можна розглянути 
:
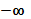