Із формули диференціала добутку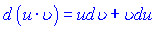 
інтегруванням двох частин рівності одержуємо формулу інтегрування частинами
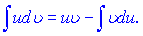
За цією формулою знаходження інтеграла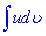 
зводиться до знаходження іншого інтеграла 
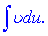Застосовувати цю формулу потрібно в тих випадках, коли інтеграл 
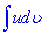легко знаходитися. Якщо неправильно вибрати 
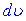, то завдання навпаки може ускладнитись. Для застосування формули інтегрування частинами до інтегралу 
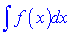необхідно підінтегральний вираз 
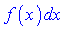представити в вигляді добутку двох множників 
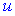та 
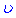. За диференціал 
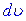завжди вибирають такий вираз, що містить 
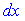. Його інтегруванням можна знайти 
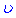. За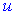 
в більшості випадків приймається функція, яка при диференціюванні спрощується.
В такий спосіб на перший погляд важкі і незрозумілі, з точки зору обчислень, інтеграли можна швидко звести до табличного вигляду.
