 |
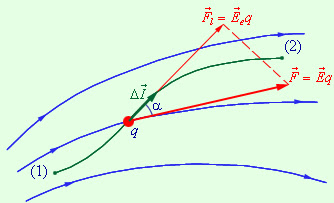
| Мал. 1 Робота електричних сил при малому переміщенні Δl заряду q. |
При переміщенні пробного заряду q в електричному полі електричні сили виконують роботу. Ця робота при малому переміщенні Δl дорівнює (мал. 1):
ΔA = F∙Δl∙cosα = qEΔlcosα = qElΔl.
Електричне поле володіє важливою властивістю:
Робота сил електростатичного поля при переміщенні заряду з одної точки поля в іншу не залежить від форми траєкторії, а визначається лише положенням початкової і кінцевої точок і величиною заряду.
Подібну властивість має гравітаційне поле, і це зрозуміло, оскільки гравітаційні та кулонівські сили описуються подібними співвідношеннями.
Наслідком незалежності роботи від форми траєкторії є наступне твердження:
Робота сил електростатичного поля при переміщенні заряда по будь-якій замкненій траєкторії дорівнює нулю.
Силові поля, які мають таку властивість, називають потенціальними або консервативними.
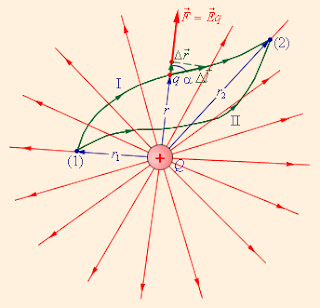 |
| Мал.2 Робота кулонівських сил при переміщенні заряду q не залежить від траекторії, а залежить лише від початкового та кінцевого положень: r1 та r2. |
На мал. 2 зображено силові лінії кулонівського поля точкового заряду Q і дві різні траєкторії переміщення пробного заряду q з початкової точки (1) в кінцеву точку (2). На одній з траєкторій виділено мале переміщення Δl. Робота ΔA кулонівських сил на цьому переміщенні дорівнює:
ΔА = FΔl∙cosα = qEΔr = QqΔr/(4πε0∙r2).
Отже, робота на малому переміщенні залежить тільки від віддалі r між зарядами і його зміни Δr. Якщо цей вираз проінтегрувати на інтервалі від r = r1 до r = r2, то отримаємо:
Отриманий результат не залежить від форми траєкторії. На траєкторіях I і II, зображених на мал. 2, роботи кулонівських сил однакові. Якщо на одній з траєкторій змінити напрям переміщення заряду q на протилежний, то робота теж змінить знак.
Звідси випливає, що на замкнутій траєкторії робота кулонівських сил дорівнює нулеві.
Якщо електростатичне поле створює декілька точкових зарядів Qi, то при переміщенні пробного заряду q робота A результуючого поля відповідно до принципу суперпозиціі буде складатися з робіт Ai кулонівських полів точкових зарядів: А = ∑Аі . Оскільки кожен член суми Ai не залежить від форми траєкторії, то і повна робота A результуючого поля не залежить від шляху і визначається лише положенням початкової і кінцевої точок траєкторії.
2°. Потенціальна енергія в електриці.
Властивість потенціальності електростатичного поля дозволяє ввести поняття потенціальної енергії заряду в електричному полі. Для цього в просторі вибирають деяку точку (0), і потенційну енергію заряду q, розташованого в цій точці, приймають рівною нулеві.
Потенціальна енергія заряду q, розташованого в будь-якій точці (1) простору, відносно фіксованої точки (0) дорівнює роботі A10, яку виконає електричне поле при переміщенні заряда q з точки (1) в точку (0):
(В електростатиці енергію прийнято позначати літерою W, так як літерою E позначають напруженість електричного поля.)
В електриці фізичний зміст має не сама потенціальна енергія, а різниця її значень в двох точках простору.
Робота, виконана електричним полем при переміщенні точкового заряду q з точки (1) в точку (2), дорівнює різниці значень потенційної енергії в цих точках і не залежить від шляху переміщення заряду і від вибору точки (0).
A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2


