Поняття про хвильову функцію та її статистична інтерпретація

Хвильова функція, або псі-функція 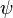$psi ,$ — комплекснозначна функція, що використовується в квантовій механіці для опису стану квантовомеханічної системи. Є коефіцієнтом розкладу вектору стану за базисом (зазвичай координатному):

$left|psi(t)rightrangle=int Psi(x,t)left|xrightrangle dx$

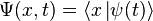де $left|xrightrangle = left|x_1, x_2, ldots , x_nrightrangle$ — координатний базисний вектор, а $Psi(x,t)= langle xleft|psi(t)rightrangle$ — хвильова функція у координатному представленні.

Опис квантової системи за допомогою функції, яка б описувала її хвильові властивості запропонував Ервін Шредінгер.

Зміст

[сховати]

Інтерпретація [ред.]

Макс Борн запропонував інтерпретувати хвильову функцію, як амплітуду ймовірності. В цій інтерпретації квадрат модуля хвильової функції відповідає густині ймовірності положення частинки. Таким чином, імовірність того, що частинка перебуває в області простору W в момент часу t визначається як

$operatorname{P}(W) = int limits_W |psi(mathbf{r},t)|^2 dW. quad$

де

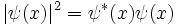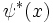$|psi(x)|^2 = psi^*(x) psi(x) quad$ , а $psi^*(x) quad$ — функція, комплексно спряжена з $psi(x) quad$

При інтегруванні по всьому простору цей вираз, як імовірність цілком певної події, повинен давати одиницю:

$int limits_{infty} |psi(mathbf{r},t)|^2 dV = 1. quad$

Ця умова має назву умови нормування псі-функції.

Значення фізичних величин [ред.]

Фізична величина, яка може визначатися в експерименті, у квантовій механіці задається певним ермітовим оператором. Знаючи хвильову функцію можна визначити середнє значення такої величини за допомогою правила

$langle A rangle = int psi^* hat{A} psi dV$ ,

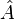де $hat{A}$ — це квантовомеханічний оператор.

Вектор стану [ред.]

Для опису елементарних частинок, які можуть мати відмінний від нуля спін, однокомпонентної, скалярної, хвильової функції недостатнью. Рух таких частинок задається сукупністю із кількох хвильових функції, яка має ширшу назву: вектор стану.

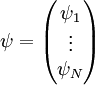$psi = left( begin{matrix} psi_1 \ vdots \ psi_N end{matrix}right)$ .

Наприклад, електрон зі спіном 1/2 описується сукупністю чотирьох хвильових функцій.

Незважаючи на слово «вектор», вектор стану не є справжнім вектором у просторі. Тут цей термін вживається радше в сенсі вектора лінійної алгебри. Щодо просторових властивостей, то при обертанні системи координат, вектор стану загалом може мати особливі властивості. Наприклад, вектор стану для електрона є спінором.

Зазвичай, сукупність кількох хвильових функцій, які входять до складу вектора стану, теж називають хвильовою функцією.

Властивості [ред.]

Хвильова функція означена з точністю до довільного множника у формі $e^{ialpha}$ , де $alpha$ - будь-яке дійсне число. Підстановка функції

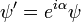
$psi^prime = e^{ialpha} psi$

не міняє середніх значень спостережуваних фізичних величин.

Хвильова функція системи багатьох частинок [ред.]

Хвильова функція квантової системи, що складається з кількох частинок, залежить від координат всіх частинок. Наприклад, для двох частинок $psi(mathbf{r}_1, mathbf{r}_2, t)$ . При визначенні середніх значень спостережуваних величин інтегрування проводиться у всьому конфігураційномі просторі. Наприклад, для двох частинок

$langle A(t) rangle = int psi^*(mathbf{r}_1, mathbf{r}_2, t) hat{A} psi(mathbf{r}_1, mathbf{r}_2, t) dV_1 dV_2$ ,

У випадку тотожності частинок, на хвильову функцію накладається додаткова умова, пов'язана з інваріантністю щодо перестановок цих частинок, згідно з принципом нерозрізнюваності. Квантові частинки поділяються на два класи - ферміони й бозони. Для ферміонів

$psi(mathbf{r}_1, mathbf{r}_2, t) = -psi(mathbf{r}_2, mathbf{r}_1, t)$ ,

тобто хвильова функція міняє знак при перестановці частинок. Таку фунцію називають антисиметричною щодо перестановок. Для бозонів

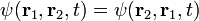$psi(mathbf{r}_1, mathbf{r}_2, t) = psi(mathbf{r}_2, mathbf{r}_1, t)$ ,

тобто при перестановці частинок хвильова функція залишається незмінною. Таку функцію називають симетричною щодо перестановок.