План скоростей

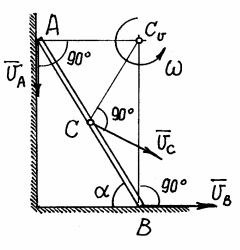
Пусть известны скорости нескольких точек плоского сечения тела (рис.38). Если эти скорости отложить в масштабе из некоторой точки О и соединить  их  концы  прямыми,  то получится картинка,  которая  называется планом скоростей. (На рисунке  ).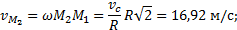

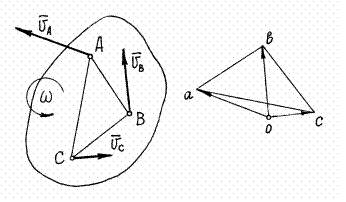
Рис.38

 

Свойства  плана скоростей.

 

Рис. 9.26.

а)  Стороны треугольников на плане скоростей перпендику­лярны  соответствующим  прямым на плоскости тела.

 

Действительно, 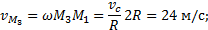. Но на плане скоростей 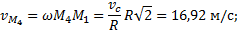. Значит  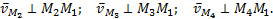причём  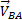 перпендикулярна  АВ, по­этому и 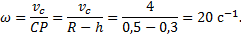.  Точно так же   и .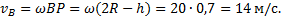

б) Стороны  плана скоростей  пропорциональны соответствующим от­резкам прямых на плоскости тела.

Так  как 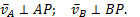 , то отсюда  и следует, что стороны  плана скоростей пропорциональны отрезкам прямых на плоскости тела.

Объединив  оба  свойства,  можно  сделать вывод,  что план скоростей подобен  соответствующей  фигуре  на  теле и повёрнут относительно её на 90˚ по  направлению  вращения.  Эти свойства  плана скоростей позволяют определять скорости точек тела графическим способом.

Пример 10. На  рисунке 39 в  масштабе  изображён  механизм. Известна угловая скорость 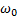 звена ОА.

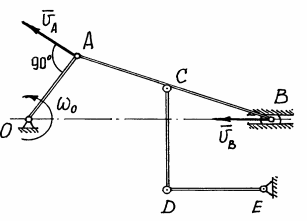
Рис.39

 

Чтобы построить план ско­ростей  должна  быть  известна скорость  какой-нибудь  одной точки  и  хотя  бы  направление вектора  скорости другой. В на­шем примере можно определить скорость точки А: 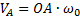 и направление  её  вектора .

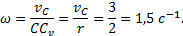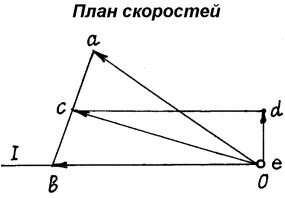
Рис.40

 

 

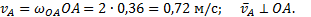Откладываем (рис. 40) из точки о в масштабе  Известно направление  вектора  скорости  ползуна  В – горизонтальное. Проводим на плане скоростей из точки О  прямую I по направлению скорости 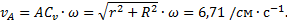, на которой  должна  находиться  точка  b, определяющая скорость этой точки В. Так  как  стороны  плана  скоростей перпендикулярны соответствующим звеньям механизма,  то  из  точки   а  проводим  прямую  перпендикулярно АВ  до  пересечения  с прямой I. Точка пересечения определит точку b, а значит и скорость точки В: 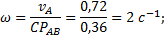. По второму свойству плана скоростей его стороны подобны звеньям  механизма. Точка С делит АВ пополам, значит и с должна делить аb пополам. Точка с определит на плане скоростей величину и направление скорости  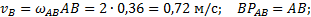(если с соединить с точкой О).

 

Скорость  точки  Е  равна  нулю, поэтому  точка е на плане скоростей  совпадает с точкой О.

Далее.  Должно  быть 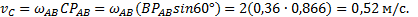  и 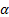. Проводим эти прямые, находим  их  точку  пересечения  d.  Отрезок  оd  определит  вектор  скорости .

 

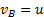Определение ускорений точек плоской фигуры

Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оxy (см.рис.30) определяется радиусом-вектором 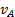 где 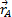. Тогда

В правой части этого равенства первое слагаемое есть ускорение 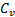 полюса А, а второе слагаемое определяет ускорение 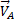,  которое точка м получает при вращении фигуры вокруг полюса A. следовательно,

.

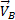Значение 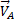, как ускорения точки вращающегося твердого тела, определяется как

, 

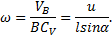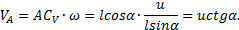
где 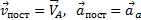 и 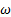 - угловая скорость и угловое ускорение фигуры, а  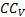- угол между вектором  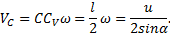и отрезком МА (рис.41).

Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения  какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка Мполучает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения 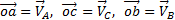, находятся построением соответствующего параллелограмма (рис.23).

Однако вычисление 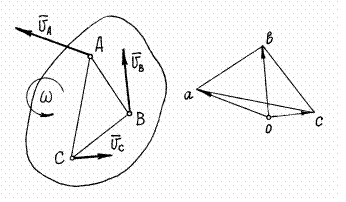с помощью параллелограмма, изображен­ного на рис.23, усложняет расчет, так как предварительно надо бу­дет находить значение угла 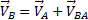, а затем - угла между векторам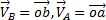и  и 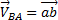,  Поэтому при решении задач удобнее вектор  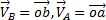 заменять его касательной  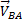и нормальной  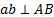составляющими и пред­ставить в виде

.

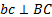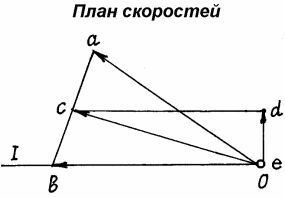
При этом вектор 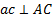 направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор  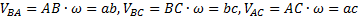всегда направлен от точки М к полюсу А (рис.42). Численно же

.

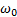Если полюс А движется не прямолинейно, то его ускорение мо­жно тоже представить как сумму касательной 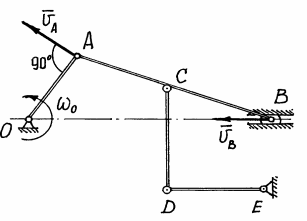  и нормальной  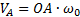составляющих, тогда

.

 

           

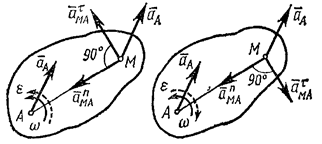
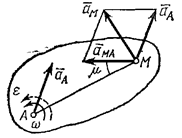
Рис.41                                                             Рис.42

 

Наконец, когда точка М движется криволинейно и ее траекто­рия известна, то 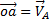можно заменить суммой .

 

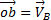Решение задач на определение ускорения

Ускорение любой точки плоской фигуры в данный  момент времени можно найти, если известны: 1) векторы скорости 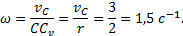  и ускорения  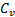какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фи­гуры. В ряде случаев вместо траектории второй точки фигуры до­статочно знать положение мгновенного центра скоростей.

Тело (или механизм) при решении задач надо изображать в том положении, для которого требуется определить ускорение соответ­ствующей точки. Расчет начинается с определения по данным задачи скорости и ускорения точки, принимаемой за полюс.

План решения (если заданы скорость и ускорение одной точки плоской фигуры и направления скорости и ускорения другой точки фигуры):

1) Находим мгновенный центр скоростей, восставляя перпендикуляры к скоростям двух точек плоской фигуры.

2) Определяем мгновенную угловую скорость фигуры.

3) Определяем центростремительное ускорение точки вокруг полюса, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

4) Находим модуль вращательного ускорения, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

5) Определяем мгновенное угловое ускорение плоской фигуры по найденному вращательному ускорению.

6) Находим ускорение точки плоской фигуры при помощи формулы распределения ускорений.

При решении задач можно применять «теорему о проекциях векторов ускорений двух точек абсолютно твердого тела»:

«Проекции векторов ускорений двух точек абсолютно твердого тела, которое совершает плоскопараллельное движение, на прямую, повернутую относительно прямой, проходящей через эти две точки, в плоскости движения этого тела на угол 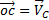в сторону углового ускорения, равны».

Эту теорему удобно применять, если известны ускорения только двух точек абсолютно твердого тела как по модулю, так и по направлению, известны только направления векторов ускорений других точек этого тела (геометрические размеры тела не известны), не известны 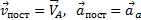 и 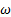 – соответственно проекции векторов угловой скорости и углового ускорения  этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела. 

Известны еще 3 способа определения ускорений точек плоской фигуры:

1) Способ основан на дифференцировании дважды по времени законов плоскопараллельного движения абсолютно твердого тела.

2) Способ основан на использовании мгновенного центра ускорений абсолютно твердого тела (о мгновенном центре ускорений абсолютно твердого тела будет рассказано ниже).

3) Способ основан на использовании плана ускорений абсолютно твердого тела.

Пример 11. Диск катится без скольжения по прямой. Центр его С имеет скорость 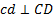 и ускорение  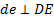(рис. 43). Найдем ускорение точки А.

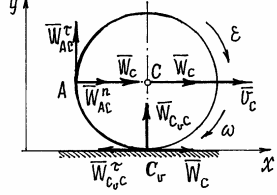
Рис.43

 

Угловую скорость находим с помощью мгновенного центра скоростей:

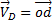
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что 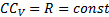, а точка С движется по прямой, получим                  

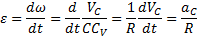
Если С – полюс, то 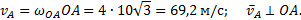, где

.

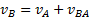
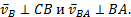Величину  ускорения  найдём  с помощью проекций на оси х и у:

 

Рис.9.30.

Тогда .

 

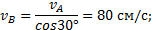
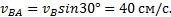Ускорение мгновенного центра скоростей ,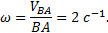

 где .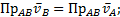 

И, так как 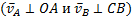, ускорение  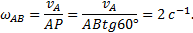  и  .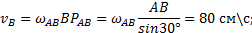

Таким  образом,  ускорение  мгновенного  центра  скоростей  не равно нулю.

Пример 12. Вернёмся к примеру 9 (рис. 44). 

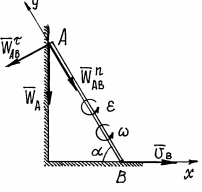
Рис.44

 

Найдём  ускорение точки А, полагая 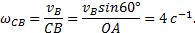 т.е.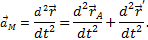 

Имеем:

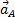,               (1)

Где 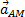,  но направление  вектора  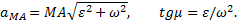неизвестно, неизвестно и угловое ускорение .   

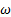Предположим,  что  вектор 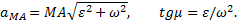 направлен перпендикулярно АВ, влево.

Ускорение 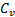, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:

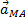   и    .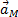

Из второго уравнения сразу находим ускорение точки А

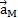
Положительное значение 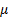  указывает на то, что направление вектора  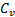выбрано правильно.

Из  первого  уравнения  можно  найти  ускорение 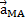 и угловое ускорение  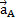 (направления  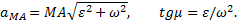и  также угаданы верно).