Векторный способ задания движения точки.
Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор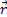 
, проведенный из начала координат О в точку М (рис. 3).
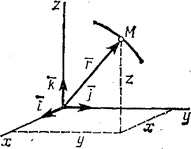
Рис.3
При движении точки М вектор 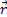будет с течением времени изменяться и по модулю, и по направлению. Следовательно, 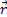является переменным вектором (вектором-функцией), зависящим от аргумента t:
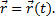
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 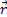и найти положение движущейся точки.
Геометрическое место концов вектора 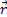, т.е. годограф этого вектора, определяет траекторию движущейся точки.
Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):
V=dr/dt (1.2)
а
б
Рисунок 1.2
Ускорение точки (изменение ее скорости) определяется как производная от скорости:
Вектор ускорения направлен по касательной к годографу вектора скорости (рисунок
