| ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ ПО ФОРМУЛЕ ЭЙЛЕРА |
| Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид: |
 |
| где Е - модуль продольной упругости материала стержня; |
| Jmin - минимальный момент инерции поперечного сечения стержня. |
| Для стержней с другими видами закрепления формулу Эйлера записывают в виде: |
 |
где  - приведенная длина стержня; |
 - коэффициент приведения длины. |
| Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению. |
| Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять |
 |
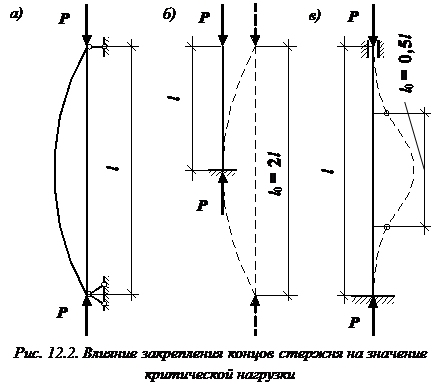
| На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента |
 |
| Рис. 8.2 |
Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение  не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости |
 |
| в свое время полученной на основании закона Гука. |
| Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна |
 |
| где |
 - минимальный радиус инерции (геометрическая характеристика сечения); |
 - минимальный момент инерции площади сечения стержня. |
Значение предельной гибкости  получается из условия |
 |
| Предельная гибкость равна |
 |
| Так, для малоуглеродистой стали, если принять Е = 2x105 МПа, |
 |
Для повышения несущей способности конструкций в них стремятся использовать стержни возможно меньшей гибкости. Так что расчет реальных конструкций с гибкостью  практически маловероятен. Будем считать  |
| верхней границей значений гибкости реальных стержней. |
| Следовательно, формула Эйлера для определения критического значения сжимающей силы в виде |
 |
| применима в случае, если гибкость стержня находится в пределах |
 |
| (кривая СД на рис. 8.3) |
 |
| Рис. 8.3 |
| Для малоуглеродистой стали этот диапазон равен |
 |
|
Л. Эйлер получил формулу для определения теоретической нагрузки (Эйлерова нагрузка), при которой происходит потеря устойчивости стержня. Формула Эйлера: ФОРМУЛА ЭЙЛЕРА ДЛЯ ШАРНИРНО-ОПЕРТОГО СТЕРЖНЯ, СЖАТОГО ПО КОНЦАМДля шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения критической нагрузки: Основной случай потери устойчивости – случай, когда при закреплении концов стержня и приложении нагрузки форма потери устойчивости представляет собой одну полуволну синусоиды (рис. 12.2, а). Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по торцам) легко могут быть приведены к основному случаю потери устойчивости путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.
ФОРМУЛА ЭЙЛЕРА ДЛЯ СТЕРЖНЯ С ЗАЩЕМЛЕННЫМ И СВОБОДНЫМ КОНЦАМИПри потере устойчивости стержень с жестко защемленным одним и свободным другим концом изогнется, как показано на (рис. 12.2, б). Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Приведенная длина равна ФОРМУЛА ЭЙЛЕРА ДЛЯ СТЕРЖНЯ С ЗАЩЕМЛЕННЫМИ КОНЦАМИДля стержня, оба конца которого жестко защемлены, форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 12.2, в). Поэтому приведенная длина стержня равна Критической ( Формула Эйлера получена из предположения, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности ( ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРАПределы применимости формулы Эйлера можно установить, предварительно введя понятие гибкости стержня. Определим эйлеровы напряжения, исходя из формулы Эйлера:
Здесь Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде: Формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня в случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен. |
 |
|
|||||||||||||||
|
I семестр:
|
Критическая сила.Формула Эйлера
|
|||||||||||||||
|
||||||||||||||||
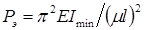, где Е – модуль Юнга; 
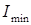– минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости); 
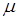– коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение 
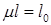- приведенная длина стержня.
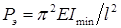(коэффициент приведения длины 
).
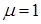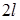(полуволна синусоиды имеет длину 
.
(
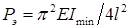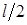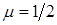), а формула эйлеровой нагрузки 
.
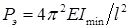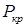) принято называть истинную, а эйлеровой (
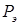) – теоретическую нагрузку, при которой происходит потеря 
: 
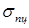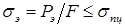. Модуль Юнга (Е) в формуле Эйлера 
.
.
.
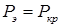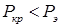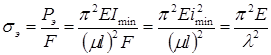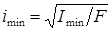– минимальный радиус инерции; 
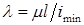–гибкость сжатого стержня: 
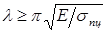. Величину в правой части неравенства обозначим 
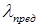и назовем предельной гибкостью. Тогда 
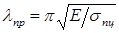. В отличие от гибкости стержня, предельная гибкость зависит только от физико-механических свойств материала и не зависит от размеров. Предельная гибкость– постоянная для данного материала величина. Например, для стали Ст. 3 
.
.
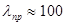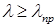