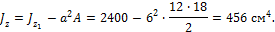9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ
Способ вычисления моментов инерции сложных сечений основан на том, что любой интеграл можно рассматривать как сумму интегралов и, следовательно, момент инерции любого сечения вычислять как сумму моментов инерции отдельных его частей.
Поэтому для вычисления моментов инерции сложное сечение разбивается на ряд простых частей (фигур) с таким расчетом, чтобы их геометрические характеристики можно было вычислить по известным формулам или найти по специальным справочным таблицам.
В ряде случаев при разбивке на простые фигуры для уменьшения числа или упрощения их формы сложное сечение целесообразно дополнять некоторыми площадями. Так, например, при определении геометрических характеристик сечения, показанного на рис. 22.5, а, его целесообразно дополнить до прямоугольника  , а затем из геометрических характеристик этого прямоугольника вычесть характеристики добавленной части
, а затем из геометрических характеристик этого прямоугольника вычесть характеристики добавленной части  . Аналогично поступают и при наличии отверстий (рис. 22.5, б).
. Аналогично поступают и при наличии отверстий (рис. 22.5, б).

Рис. 22.5
После разбивки сложного сечения на простые части для каждой из них выбирается прямоугольная система координат, относительно которой надо определить моменты инерции соответствующей части. Все такие системы координат принимаются параллельными друг другу для того, чтобы затем путем параллельного переноса осей можно было подсчитать моменты инерции всех частей относительно системы координат, общей для всего сложного сечения.
Как правило, система координат для каждой простой фигуры принимается центральная, т. е. ее начало совпадает с центром тяжести этой фигуры. В этом случае последующий подсчет моментов инерции при переходе к другим параллельным осям упрощается, так как формулы перехода от центральных осей имеют более простой вид, чем от нецентральных.
Следующим этапом является вычисление площадей каждой простой фигуры, а также ее осевых и центробежного моментов инерции относительно осей выбранной для нее системы координат. Статические моменты относительно этих осей, как правило, равны нулю, так как для каждой из частей сечения эти оси обычно являются центральными. В случаях, когда это нецентральные оси, необходимо вычислять статические моменты.
Полярный момент инерции вычисляется только для круглого (сплошного или кольцевого) сечения по готовым формулам; для сечений других форм эта геометрическая характеристика не имеет какого-либо значения, так как при расчетах она не используется.
Осевые и центробежный моменты инерции каждой простой фигуры относительно осей ее системы координат подсчитываются по имеющимся для такой фигуры формулам или таблицам. Для некоторых фигур имеющиеся формулы и таблицы не позволяют определить необходимые осевые и центробежный моменты инерции; в этих случаях приходится пользоваться формулами перехода к новым осям (обычно для случая поворота осей).
В таблицах сортамента величины центробежных моментов инерции для уголков не указаны. Методика определения таких моментов инерции рассмотрена в примере 4.5.
В подавляющем большинстве случаев конечной целью вычисления геометрических характеристик сечения является определение его главных центральных моментов инерции и положения главных центральных осей инерции. Поэтому следующим этапом вычисления является определение координат центра тяжести заданного сечения [по формулам (6.5) и (7.5)] в некоторой произвольной (случайной) системе координат  Через этот центр тяжести сечения проводятся вспомогательные (не главные) центральные оси
Через этот центр тяжести сечения проводятся вспомогательные (не главные) центральные оси  параллельные осям системы координат простых фигур.
параллельные осям системы координат простых фигур.
Затем с помощью формул, устанавливающих зависимости между моментами инерции для параллельных осей (см. § 5.5), определяются моменты инерции каждой простой фигуры относительно вспомогательных, центральных осей  Путем суммирования моментов инерции каждой простой фигуры относительно осей
Путем суммирования моментов инерции каждой простой фигуры относительно осей  определяются моменты инерции всего сложного сечения относительно этих осей; при этом моменты инерции отверстий или добавленных площадок вычитаются.
определяются моменты инерции всего сложного сечения относительно этих осей; при этом моменты инерции отверстий или добавленных площадок вычитаются.
Угол  характеризующий положение главных осей инерции, и величины главных моментов инерциивычисляются по формулам (36.5) и (38.5) или определяются графически — с помощью круга Мора (см. § 8.5). После вычисления величин
характеризующий положение главных осей инерции, и величины главных моментов инерциивычисляются по формулам (36.5) и (38.5) или определяются графически — с помощью круга Мора (см. § 8.5). После вычисления величин  рекомендуется проверить, соблюдается ли равенство
рекомендуется проверить, соблюдается ли равенство  — при этом следует иметь в виду, что соблюдение этого равенства
— при этом следует иметь в виду, что соблюдение этого равенства  не гарантирует правильности вычисления значений
не гарантирует правильности вычисления значений 
Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
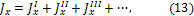
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
Пример 4.
Определить осевые моменты инерции фигуры, приведенной на рис. 4.13, относительно центральных осей zc и yc.
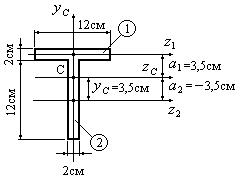
Рис.4.13
Решение:
В примере 2 для изображенной на рис.4.13 фигуры было определено положение центра тяжести С. Координата центра тяжести откладывалась от оси z2 и составила yc =3,5 см. Вычислим расстояния a1 и a2между осями z1 и zc и осями z2 и zc. Эти расстояния составили соответственно a1 =3,5 см и a2 = -3,5 см. Так как исходные оси z1 и z2 являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси zc воспользуемся формулой.
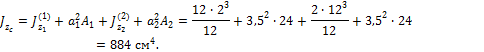
Момент инерции относительно оси yc получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось yc является общей центральной осью для простых фигур и для всей фигуры.
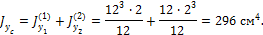
Центробежный момент инерции относительно осей zc и yc равен нулю, так как ось инерции yc является главной осью (осью симметрии фигуры).
Пример 5.
Определить момент инерции сечения, показанного на рис. 4.14, относительно оси симметрии, a=10 см.
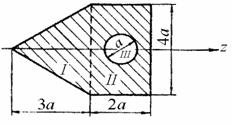
Рис.4.14
Решение.
Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг.
Момент инерции сложной фигуры относительно оси z согласно формуле (13):
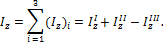
Определяем моменты инерции слагаемых простейших элементов:
Для равнобедренного треугольника:
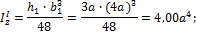
для прямоугольника согласно формуле:
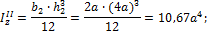
для круга согласно формуле:
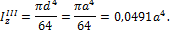
Окончательно получим:
Iz= 4,0a4 + 10,67a4 - 0,0491a4 = 14,6a4 = 14,6×104 = 1,46×105 см4.
Пример 6.
Определить момент инерции симметричного сечения, показанного на рис. 4.15, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
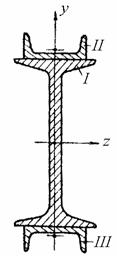
Рис.4.15
Решение.
Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры.
По сортаменту на стандартные прокатные профили имеем:
Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4.
Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см.
Момент инерции сечения относительно оси y согласно (13)
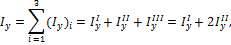
т.к. оба швеллера расположены идентично относительно оси y.
Для двутавра 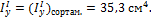
Для швеллера 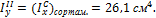
Окончательно имеем: 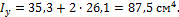
Пример 7.
Чему равен размер b (в см) фигуры, изображенной на рис. 4.16, если момент инерции фигуры относительно оси z1 равен 1000 см4?
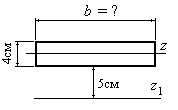
Рис.4.16
Решение.
Выразим момент инерции относительно оси z через неизвестный размер сечения b, воспользовавшись формулами (12), учитывая, что расстояние между осями z и z1 равно 7 см:
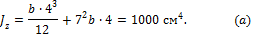
Решая выражение (а) относительно размера сечения b, получим:
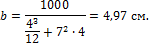
Пример 8.
Какая из фигур, изображенных на рис.4.17, имеет больший момент инерции относительно оси z, если обе фигуры имеют одинаковую площадь A=400 см2?
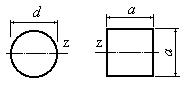
Рис.4.17
Решение.
1. Выразим площади фигур через их размеры и определим:
а) диаметр сечения для круглого сечения:
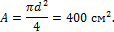
Откуда
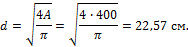
б) размер стороны квадрата:
A = a2.
Откуда
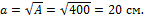
2. Вычисляем момент инерции для круглого сечения:
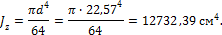
3. Вычисляем момент инерции для сечения квадратной формы:
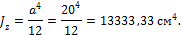
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 9.
Определить полярный момент инерции (в см4) сечения прямоугольной формы относительно его центра тяжести, если ширина сечения b=8 см, высота сечения h=24 см.
Решение.
1. Найдем моменты инерции сечения относительно горизонтальной z и вертикальной y центральных осей инерции:
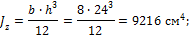
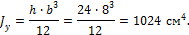
2. Определяем полярный момент инерции сечения как сумму осевых моментов инерции:
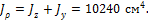
Пример 10.
Определить момент инерции фигуры треугольной формы изображенной на рис.4.18, относительно центральной оси z, если момент инерции фигуры относительно оси z1 равен 2400 см4.
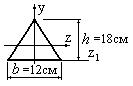
Рис.4.18
Решение.
Момент инерции сечения треугольной формы относительно главной оси инерции z будет меньше по сравнению с моментом инерции относительно оси z1 на величину a2A. Поэтому при a = h/3 = 6 см момент инерции сечения относительно оси z найдем следующим образом: