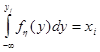. (7)
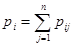Моделирование случайных векторов.Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, описываемыми совместным законом распределения. Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (x, h) является дискретной и ее составляющая принимает возможные значения x1, x2, …, xn, а составляющая h — значения y1, y2, …, yn, причем каждой паре (xi, yj) соответствует вероятность рij. Тогда каждому возможному значению xi случайной величины x будет соответствовать .
Тогда в соответствии с этим распределением вероятностей можно определить конкретное значение xiслучайной величины x (по правилам, рассмотренным ранее) и из всех значений pij выбрать последовательность
(8) которая описывает условное распределение величины h при условии, что x = xi.Затем определяем конкретное значение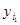 
случайной величины h в соответствии с распределением вероятностей. Полученная пара 
будет первой реализацией моделируемого случайного вектора. Далее определяем возможные значения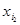 
, выбираем последовательность
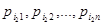(9)
и находим 
в соответствии с распределением (9). Это дает реализацию вектора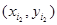 
и т. д.
Рассмотрим моделирование непрерывного случайного вектора с составляющими x и h.В этом случае двухмерная случайная величина (x, h) описывается совместной функцией плотности f(х, у).Эта функция может быть использована для определения функции плотности случайной величины как
Имея функцию плотности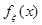 
, можно найти случайное число хi, а затем при условии, что x = хi, определить условное распределение случайной величины h:
В соответствии с этой функцией плотности можно определить случайное число уi. Тогда пара чисел (xi, yi) будет являться искомой реализацией вектора (x, h).
Рассмотренный способ формирования реализаций двухмерных векторов можно обобщить и на случай многомерных случайных векторов. Однако при больших размерностях этих векторов объем вычислений существенно увеличивается, что создает препятствия к использованию этого способа в практике моделирования систем.
