15

Сетевые модели  (N-схемы 

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри.

Теория сетей Петри развивается в нескольких направлениях:

1.   разработка математических основ,

2.   структурная теория сетей,

3.   различные приложения (параллельное программирование, дискретные динамические системы и т. д.).

Формально сеть Петри (N-схема) задается четверкой вида

,

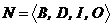где В — конечное множество символов, называемых позициями ,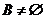

D — конечное множество символов, называемых переходами, , ;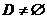

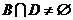I — входная функция (прямая функция инцидентности) ;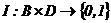

О — выходная функция (обратная функция инцидентности), .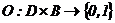

Таким образом, входная функция I отображает переход dj в множество входных позиций 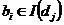, а выходная функция О отображает переход dj в множество выходных позиций 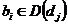. Для каждого перехода  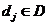можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О(dj) как

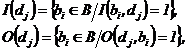
Аналогично, для каждого перехода 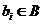 вводятся определения множества входных переходов позиции I(bi) и множества выходных переходов позиции O(bi):

.

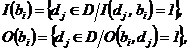Графически N-схема изображается в виде двудольного ориентированногомультиграфа, представляющего собой совокупность позиций и переходов  (рис. 1).

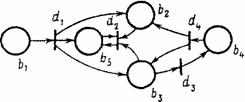
Рис. 1. Графическое изображение N-схемы

Как видно из этого рисунка, граф N-схемы имеет два типа узлов: позиции и переходы, изображаемые 0 и 1 соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или перехода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.

Приведенное представление N-схемы может использоваться только для отражения статики моделируемой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки) .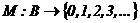

Маркировка М есть присвоение неких абстрактных объектов, называемых метками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графическом задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры).

Маркированная (размеченная) N-схема может быть описана в виде пятерки  и является совокупностью сети Петри и маркировки М.

Функционирование N-схемы отражается путем перехода от разметки к разметке. Начальная разметка обозначается как 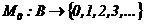. Смена разметок происходит в результате срабатывания одного из переходов  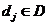сети. Необходимым условием срабатывания перехода dj является 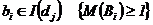, где 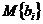, - разметка позиции bi. Переход dj для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход.

Срабатывание перехода изменяет разметку сети М(b) = (М(b1), М(b2), ..., M(bn))2 на разметку М¢(b) по следующему правилу:

M'(b) = M(b)-I(dj) + O(dj)

т. е. переход dj изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций.

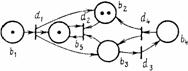
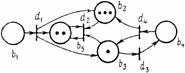
Рис. 2. Пример функционирования размеченной N-схемы

Важной особенностью моделей процесса функционирования систем с использованием типовых N-схем является простота построения иерархических конструкций модели. С одной стороны, каждая N-схема может рассматриваться как макропереход или макропозиция модели более высокого уровня. С другой стороны, переход, или позиция N-схемы, может детализироваться в форме отдельной подсети для более углубленного исследования процессов в моделируемой системе S.

Типовые N-схемы на основе обычных размеченных сетей Петри пригодны для описания в моделируемой системе S событий произвольной длительности. В этом случае модель, построенная с использованием таких N-схем, отражает только порядок наступления событий в исследуемой системе S. Для отражения временных параметров процесса функционирования моделируемой системы S на базе N-схем используется расширение аппарата сетей Петри: временные сети, E-сети.

Моделирование случайных воздействий на систему

При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преоб­разованию последовательностей случайных чисел.

Моделирование случайных событий.Пусть имеются случайные числаxi т. е. возможные значения случайной величины x, равномерно распределенной в интервале (О, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение xi, случайной величины x удовлет­воряет неравенству  . (1)

Тогда вероятность события А будет 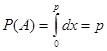 Тогда  .

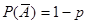Процедура моделирования в этом случае состоит в выборе значений xi,и сравнении их с р. При этом, если условие (1) выполняется, исходом испытания является событие А.

Таким же образом можно рассмотреть группу событий. Пусть A1, A2, …, As — полная группа событий, наступающих с вероят­ностями p1, p2, …, ps, соответственно. Определим Аm как событие, состоящее в том, что выбранное значение xi случайной величины x удовлетворяет неравенству

 , (2) где 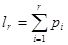 .Тогда  .

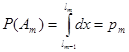Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел xi, со значениями lr . Исходом испытания оказывается событие Аm, если выполняется условие (2). Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p1, p2, …, ps.

Эти процедуры моделирования были рассмотрены в предполо­жении, что для испытаний применяются случайные числа xi, имеющие равномерное распределение в интервале (О, 1). При моделировании на ЭВМ используются псевдослучайные числа с квазиравномерным распределением, что приводит к некоторой ошибке.

Моделирование непрерывных случайных величин.Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина h задана интегральной функцией распределения

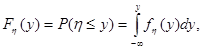
где  — плотность вероятностей.

можно воспользоваться методом обратной функции. Взаимно однозначна монотонная функция  , полученная решением относительно h уравнения 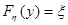 , преобразует равномерно распределенную на интервале (О, 1) величину x вh с требуемой плотностью  .

Действительно, если случайная величина h имеет плотность рас­пределения  , то распределение случайной величины

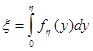
является равномерным в интервале (О, 1). Чтобы получить число, принад­лежащее последовательности случайных чисел